Dice for playing games are manufactured in a broad and ever-growing variety. One kind, however, is so widely used and well known that it deserves to be recognized as the standard. Its key features are:

• Each die is a cube, except that the edges are uniformly rounded.
• The dice are made of a rigid material.
• Sizes vary, but typical dice measure about two centimeters along the edge.
• Each face has several markings, called spots or pips. Often the spots are circular depressions molded into the cube.
  • The spots are readily visible, being painted in a color contrasting the die body.
  • All spots on a die are of the same size, shape and color.
  • Each face has a different number of spots, from one to six.
  • Any pair of opposite faces has a total of seven spots.
• A die is manufactured so that when thrown (the usual term is rolled) onto a level surface, each of the six faces has an equal probability of being on top when the die comes to rest.
• In games that use multiple dice, all dice are identical.

Below are shown views of a standard die from several different vantage points. If a person is holding a die so that the two-spot is on the left and the three-spot is on the right, the one-spot should be on the top, as in the leftmost image.

Standard

If instead the six-spot appears on top, as below, the die is a mirror image of the standard -- but there are few if any games where this distinction actually matters.

Non-standard

It is possible to rotate the two-, three- and six-pip faces by ninety degrees, as below, but this also should not affect the playing of any game.

Standard	Non-standard

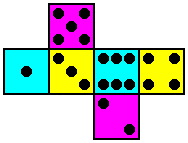
Useful is the "unfolded" digram, because it shows all six faces at once. Below is the standard die:

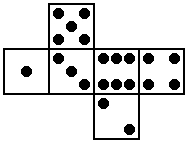
Among the more patently non-standard dice are seen the following:

• Dice that are not cubes, but instead have four, eight, ten, twelve or twenty faces; these are usually marked with numerals instead of spots.
• Dice that bear depictions of higher-ranking playing cards instead of spots.
• Dice on which the spots are not all painted in the same color.

One example of a game with special dice is Kismet, originally copyrighted by Lakeside Games, in which the dice are standard except in the coloring of the spots. While all the spots within each face are still uniform in color, different faces use different colors: ones and sixes are black, twos and fives are red, threes and fours are green. In total there are five dice, all identical. This arrangement has some elegant features:

• Opposite faces are the same color
• Adjacent faces are different colors.
• Each die has a total of seven spots in each color.
• The colors red, black and green recall a roulette wheel, or the black and red pips of playing cards in conjunction with the green surface of many gaming tables.
• Five is the quantity of dice for numerous games.

Kismet is derived from the traditional game of Yacht, which uses five dice that are standard in all regards. We do not attempt to list all the scoring possibilities, but in either game a player earns points by rolling combinations of dice such as a straight (2-3-4-5-6) or full house (three dice of one number and two of another). Kismet, with its tricolor dice, allows the rulemaker additional options. For example, some full houses involve one color (as with 2-2-2-5-5, all red) while others involve two (as with 2-2-2-6-6, red and black); Kismet gives bonus points for the full house in one color.

Yacht is itself derived from the game of Poker Dice, where the object is to roll poker-style hands, while Yahtzee is a commercial adaptation of Yacht. Poker Dice is often played with cubic dice displaying not the usual spots but instead compact representations of playing cards.

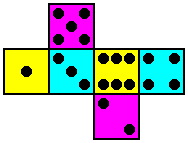
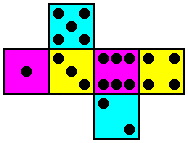
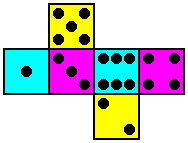
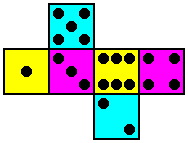
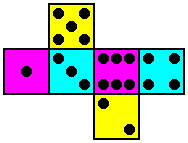
We propose a variation on the Kismet design, using six dice instead of five. Named Permucolor (from permutations of colors), each of its dice is the standard cube as described above except for the coloration of its faces. In fact, each die has a different coloring scheme. While all the spots are black, the backgrounds of the faces are three different colors -- yellow, magenta and cyan were chosen because they provide substantial contrast. There is a high level of symmetry in this plan:

• Each number is yellow on two dice, magenta on two dice, and cyan on two dice.
• Opposite faces are the same color, and adjacent faces different.
• Each die has a total of seven spots on each color.

Table One -- Spot Version
Die #1 1 and 6 yellow 2 and 5 magenta 3 and 4 cyan	Die #2 3 and 4 yellow 1 and 6 magenta 2 and 5 cyan	Die #3 2 and 5 yellow 3 and 4 magenta 1 and 6 cyan
Die #4 3 and 4 yellow 2 and 5 magenta 1 and 6 cyan	Die #5 1 and 6 yellow 3 and 4 magenta 2 and 5 cyan	Die #6 2 and 5 yellow 1 and 6 magenta 3 and 4 cyan

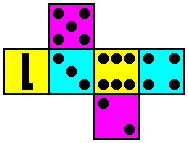
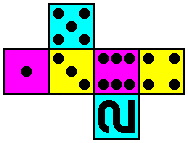
Since the six dice are similar but not identical, there is the risk that a player might not notice when there is an defect in the composition of the set. As an example, a cheater might remove die #3 and replace it with an additional die #4. (For that matter, a similar error might occur honestly at the factory.) This discrepancy will affect the odds of rolling some combinations, and the cheater stands to win handily if the honest player does not realize that anything is wrong. One way to address this weakness is to substitute on one face of each die a numeral for the spots, as in table two, giving the numeral version of the permucolor set.

Table Two -- Numeral Version
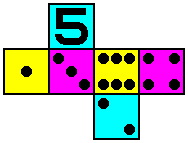
Die #1	Die #2	Die #3
Die #4	Die #5	Die #6

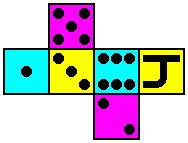The intention is that in the play of a game each numeral-style face and its spot-style counterpart be considered fully equivalent for all purposes. However, some schools of players might see benefit in regarding numerals and spots distinct, and one reasonable option is to give numerals priority over spots in deciding rolls that are otherwise tied.

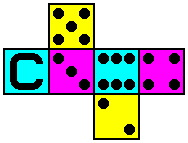
Another way to make the dice conspicuously distinct is by substituting for each one-spot a letter of the alphabet, yielding the letter version appearing in table three:

Table Three -- Letter Version
Die #1	Die #2	Die #3
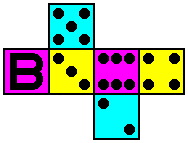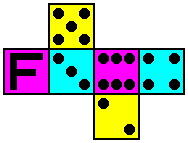
Die #4	Die #5	Die #6

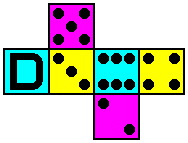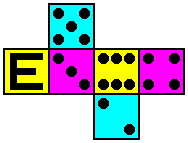Certain problems are characteristic of dice, and lettering will not solve them. The wise player will be on the lookout for a die that has, for instance, an extra 2-spot in place of the 5-spot. This device works because the 2 and the 5 are never visible simultaneously on an honest die, making the switch easy to miss, although the trick will be caught by players who are on the lookout for the mirror-image dice mentioned above. Even if all the markings are right, dice can still be phony. Some dishonest dice are of bad geometry, either by failing to be true cubes or by having some corners rounded more than others; others have weights inside. Either way, some numbers or colors will appear more often than they should, and the cheater who knows this can take advantage.

Since all six dice are different, greater variety is possible than in Kismet. For instance, one might roll a straight (1-2-3-4-5-6) all in one color, which is impossible in Kismet. Hence when fully specifying a Permucolor roll one must list color as well as number; the obvious abbreviations are Y for yellow, M for magenta and C for cyan. For a detailed example, a player might roll six dice and obtain two 1's, two 2's and two 3's, but to write this as 1-1-2-2-3-3 leaves out a great deal of information. Here are some possibilities, using the letters of table three to identify the dice:

• With dice A-E-C-F-B-D, the roll is 1Y-1Y-2Y-2Y-3Y-3Y and has one color.
• With dice A-F-C-D-B-E, the roll is 1Y-1M-2Y-2M-3Y-3M and has two colors.
• With dice A-B-C-D-E-F, the roll is 1Y-1M-2Y-2M-3M-3C and has three colors.

Rulemakers can decide what dispositions of color and number will earn high scores, but tradition suggests recognizing combinations with (1) several dice of the same number, (2) several dice of sequential number, and (3) several dice of the same color.

Horizontal combinations involve several dice with the same number.

Table Four -- Horizontal Combinations
Designation	Example	Comments
H6	3-3-3-3-3-3	All six dice have the same number
H51	2-2-2-2-2-4	Five dice bear one number; the other die is different
H42	1-1-1-1-3-3	Four dice with one number, two dice with another
H411	2-2-2-2-1-5	Four of one number, two of others
H33	5-5-5-6-6-6	Two sets of three
H321	4-4-4-2-2-5	Three of one number, two of another, one of a third
H3111	4-4-4-5-2-1	Three of one number and three of different numbers
H222	4-4-5-5-6-6	Three pairs
H2211	3-3-2-2-5-6	Two pairs
H21111	1-1-3-4-5-6	One pair
H111111	1-2-3-4-5-6	All different

Vertical combinations involve several dice with sequential numbers, and by default would be subject to multiple interpretations. For instance, a roll of 1-2-2-3-3-4 might be viewed as 1-2-3 and 2-3-4 or as 1-2-3-4 and 2-3. Our convention is to find the longest possible straight among all six dice, then the longest possible straight among the remaining dice, et cetera. With that, we prefer 1-2-3-4 and 2-3. As an another example, in a roll of 3-4-4-5-5-5 we first extract 3-4-5 leaving 4-5-5. From 4-5-5 we take 4-5 leaving 5, and the designation is V321.

The tables do not distinguish whether one straight is interior or exterior to another. In 1-2-3-5-6-6, the 5-6 straight is exterior to the 1-2-3 straight, because all the numbers are different. On the other hand, with 1-2-2-3-3-6 the 2-3 straight is interior to the 1-2-3 straight because they have numbers in common; but the 6 is exterior to both.

Table Five -- Vertical Combinations
Designation	Example	Comments
V6	1-2-3-4-5-6	Same as an H111111
V51	1-2-3-4-5-2	A sequence of five dice, with one leftover
V42	1-2-3-4-2-3	A sequence of four, and a sequence of two
V411	3-4-5-6-1-5	A sequence of four, and two unrelated dice
V33	2-3-4-2-3-4	Two sequences of three; it works out that this must also be an H222
V321	2-3-4-3-4-6	A sequence of three, another of two, and one leftover
V3111	3-4-5-3-5-1	A sequence of three
V222	2-3-2-3-5-6	Three sequences of two -- at least two of the sequences will be equal
V2211	1-2-1-2-4-6	Two sequences of two
V21111	1-2-2-2-2-2	One sequence of two
V111111	2-2-2-5-5-5	No consecutive numbers

Chromatic combinations involve several dice of the same color, and resemble horizontal combinations.

Table Six -- Chromatic Combinations
Designation	Example	Comments
C6	Y-Y-Y-Y-Y-Y	All the same color
C51	M-M-M-M-M-C	Five of one color
C42	M-M-M-M-Y-Y	Four of one color, two of another
C411	C-C-C-C-M-Y	Four of one color
C33	Y-Y-Y-M-M-M	Three in each of two colors
C321	C-C-C-Y-Y-M	Three of one color and two of another
C222	Y-Y-C-C-M-M	Three pairs in different colors

There are 46,656 different rolls of the six permucolor dice, and each falls into one the horizontal categories above, one of the vertical, and one of the chromatic. It is easy to visualize a three-dimensional table listing the number of rolls by intersection of categories. Such a diagram would for example list that there are 288 rolls that qualify as all of H2211, V321 and C42, but none that satisfy all of H31111, V51 and C33. Because it is difficult to display a three-dimensional table on a web page we have instead prepared two-dimensional slices of that table horizontally, vertically and chromatically.

For a simpler game, players can use three dice instead of all six. We recommend either dice #1, #2 and #3; or dice #4, #5 and #6. With either of these triads (and none other), each of the pip counts one through six is yellow on one die, magenta on one die, and cyan on one die. This yields as much symmetry as possible.

With three dice there are 216 different rolls, and they can be elaborated in tables similar to (though much smaller than) those for six dice.