Version of 13 November 2007

§1. A sesquidomino is like a regular domino, except it has three numbers instead of two (sesqui- is a Latin prefix meaning one-and-a-half). The term sesquidominoes can refer to either the playing equipment (each piece called a tile) or the games played therewith. Here are some examples of the tiles:

table 1A	image	symbol	category
		5-5-5	triple all are the same
		6-6-8	inside double the middle is the same as one end
		4-1-4	outside double both ends are the same
		2-3-7	single all are different

Another notation for 2-3-7 is 7-3-2; generally the symbol that starts with the smaller number is preferred. As with dominoes, no two tiles in a set of sesquidominoes will be identical. However, two tiles with the same numbers in a different sequence can co-exist, for instance 4-0-9 and 0-4-9, or 3-3-7 and 3-7-3.

If the physical tiles are of a size comparable to the usual dominoes, they will be around 25 millimeters ≈ 1 inch wide, 75 mm ≈ 3 in long, and 10 mm ≈ 0.4 in thick.

Sesquidominoes differ from triomonoes, which are equilateral triangles. Also to be distinguished are trominoes, which do not have pips (also called dots or spots) assigned to their cells, but where the three cells are sometimes arranged in a right angle.

This page gives general guidance on how to use the sesquidominoes, not the mechanics of any particular game. Of course, there are no "official" rules — rather, players are free to do whatever they can agree on.

§2. Each of the three cells can easily have anywhere from zero to nine pips. More can be squeezed in if the dots have smaller diameter, although the patterns will become more complicated. Because there are three cells, rather than the two of ordinary dominoes, the number of possible tiles in a set of sesquidominoes grows quickly as the maximum number of pips increases. For that reason, more than nine pips are not likely to be required.

table 2A	pip counts	number of tiles
		triples	inside doubles	outside doubles	singles	total
	0, 1, 2	3	6	6	3	18
	0, 1, 2, 3	4	12	12	12	40
	0…4	5	20	20	30	75
	0…5	6	30	30	60	126
	0…6	7	42	42	105	196
	0…7	8	56	56	168	288
	0…8	9	72	72	252	405
	0…9	10	90	90	360	550
	0…n	n + 1	n × (n + 1)	n × (n + 1)	(n − 1) × n × (n + 1) ÷ 2	(n + 1)2 × (n + 2) ÷ 2

For variety or simplicity, players can omit some categories of tiles and make a smaller set; for instance the single tiles form a balanced group. If zero-pip tiles are deemed undesirable, players can use the numerical range 1…n+1 rather than 0…n and get an equivalent set.

For a full example, table 2B shows the triple-four set, which has all 75 pieces that have pip counts 0 through 4:

table 2B	triples
	inside doubles
	outside doubles
	singles

Complete sets of other sizes.

§3. Suggested is a playing surface (heavy paper will suffice) printed with a grid to ensure proper alignment of the tiles in sprawling arrangements — and to prevent excessive sprawling. There is no particular constraint on the size or shape, except that the grid should be large enough to prevent undue congestion. Figure 3A below contains three examples of playing areas, rendered at half the scale of the tile examples above.

figure 3A

§4. In typical domino games, and by extension sesquidominoes, tiles are laid on the table one at a time by the players in rotation. The light-colored squares at the center of the grid mark the likely spot for laying the first tile. Thereafter, each tile is placed adjacent to some previously laid tile.

The usual rule in dominoes is that adjoining tiles must match in number of pips where they touch. How this works out in sesquidominoes, when each tile is regarded as three cells, is this: whenever two cells of adjoining tiles are edgewise adjacent, they must have the same number of pips. There is, however, no restriction on cornerwise adjacency.

If one end of one sesquidomino matches one end of another, and no other cells match, then there are seven ways that they can fit each other. Figure 4A employs 1-2-3 in fixed attitude and 3-4-5 placed in various ways, with the matches lettered for reference:

figure 4A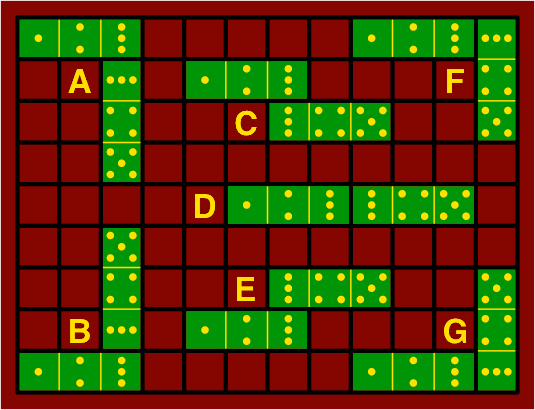

If the center number of one tile matches the end number of another, there are two ways for them to fit:

figure 4B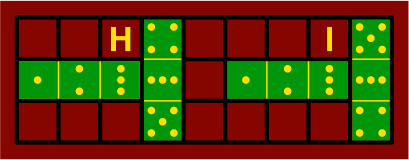

With two matching numbers suitably arranged, the arrangement of figure 4C is possible:

figure 4C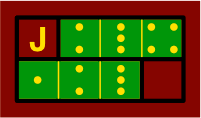

In the lower right-hand corner of figure 4D, the 1 and the 8 exemplify cornerwise adjacency of unequal numbers:

figure 4D

Not out of the question is to devise a game that uses ordinary two-cell dominoes in conjunction with these three-cell pieces.

§5. So far, the only limitation on arranging tiles is that each must be adjacent to a previously-laid file, and adjoining cells must have matching numbers. If players find that this offers too little restriction, and play becomes trivial, a saturation rule may help: each cell of a tile may have at most one neighboring tile. A result will be that each tile will never have more than three neighbors. In figure 5A, 1-2-3 is saturated with three neighbors in two ways:

figure 5A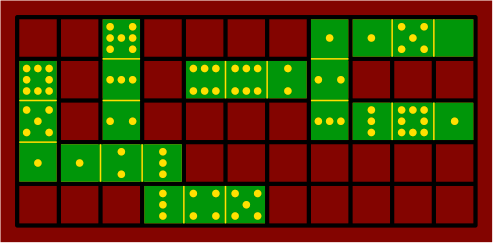

Figure 5B reveals how two neighbors can be enough to saturate 1-2-3:

figure 5B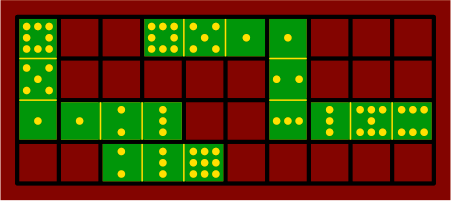

The saturation rule will most likely be helpful in the blocking games, where each player's goal is to get rid of his tiles as quickly as possible.

§6. The pip arrangements vary in their symmetry; some when rotated 90 degrees become different, others do not:

table 6A	0	1	2	3	4	5	6	7	8	9

Besides adopting the saturation rule, players might opt to prohibit the adjacency of same-number cells when that number is 2, 3, 6 or 7, and they are turned different directions. Under this parallelism rule, arrangements A, B, F, G, H and I from above would be permitted only when the common number is 0, 1, 4, 5, 8 or 9. By contrast, arrangements C, D, E and J would always work. To have different rules for different numbers is a novel restriction for occidental (contrasted to oriental) dominoes.

§7. Not yet mentioned is that the three cells of a sesquidomino can be manufactured as a right angle (a bent). There are six ways to arrange three different numbers on a bent tile, and the arrangements can be organized into three mirror-image pairs. By contrast, there are only three ways to arrange the same numbers on a straight tile.

In table 7A, the bent tiles are displayed obliquely, in the orientation of the letter 'V', so that the pip counts on the tile, when read from left to right, will give the numbers of the symbol in the correct sequence.

table 7A
	7-3-4	3-4-7	4-7-3
	4-3-7	7-4-3	3-7-4

Similarly, there are two bent varieties of each inside double. However, the outside double and the triple yield only one bent variety each.

The pip pattern in the corner cell of a bent will sometimes be different from what has been presented so far. With 2, 3, 6 or 7 pips, the design will be a mitered combination of two orientations. For other numbers of pips, nothing unusual happens. The cutting lines of mitering are shown in black in figure 7B.

figure 7B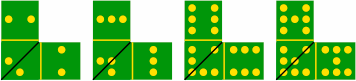

Shown in figure 7C are the traditional layouts of 2 or 3 pips for dominoes (and dice), which do not miter well, which failure is why they have not been retained for sesquidominoes.

figure 7C	versus	versus

Figure 7D is an example of how bent and straight tiles can be combined into a layout. It observes the saturation rule of §5, but not the parallelism rule of §6, which would be hard to implement for the corner cells of tiles.

figure 7D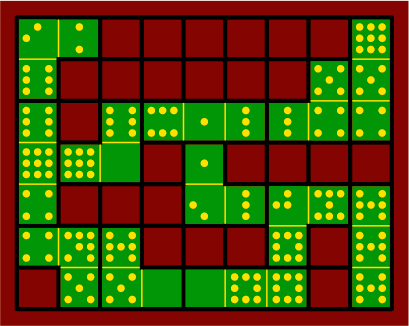

Not all genres of domino games permit the tiles to be formed into loops; those that do, however, often award bonus points to the player who completes one.

§8. An alternate board design (drawn at half-scale, as figure 3A) resembles a basketweave:

figure 8A

Tiles are installed as in figure 8B, the 'X' squares remaining empty:

figure 8B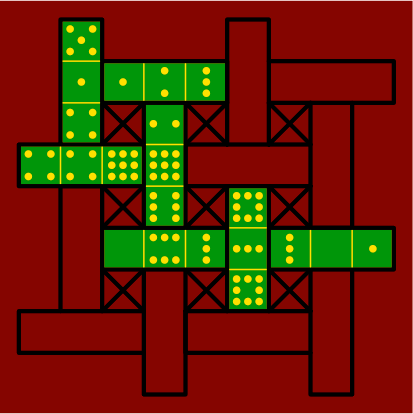

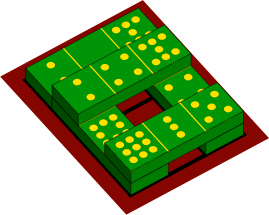
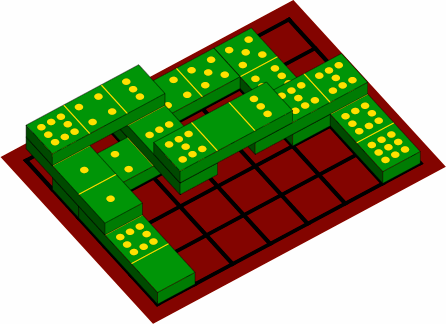
§9. Sesquidominoes are well suited to multilevel use. Figure 9A is a pictorial view of an example constructed according to the rule that an upper-level cell must have the same number of pips as the cell below it.

figure 9A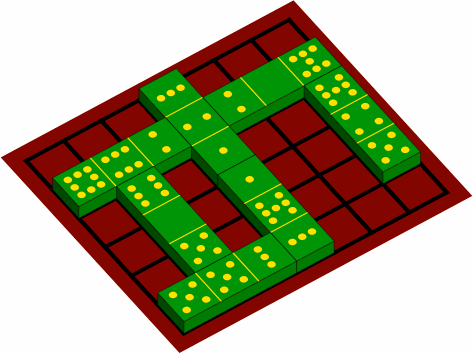

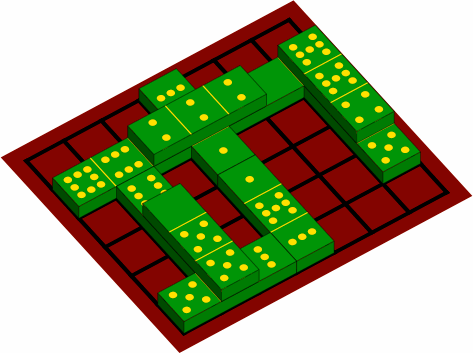
It will rarely be possible to have a second level that completely covers a first level of much complexity.

With its three cells, a sesquidomino is physically capable of spanning a gap, as in figure 9B. Players will have to decide whether this is a good idea.

figure 9B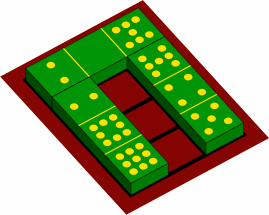

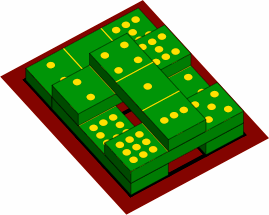
In figure 9B, the unsupported cell of a sesquidomino is in the middle, and a stable arrangement ensues. If instead the unsupported cell is on one end (figure 9C), the layout risks becoming mechnically unstable, falling down as further layers are added. Hence players will likely prohibit cantilevering.

figure 9C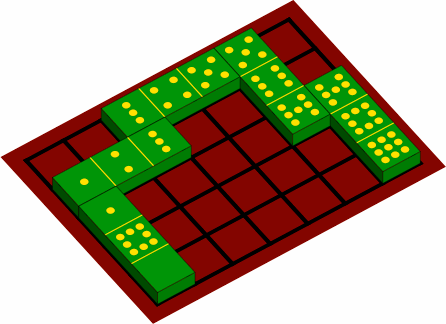

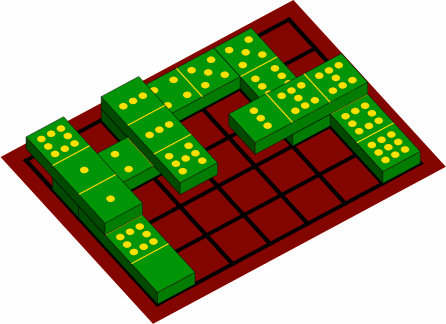
§10. Although dominoes usually have square cells, triangles work equally well. Each cell can easily contain as many as six pips. Although this is less than the nine of square cells, a sesquidomino with three triangular cells is asymmetric, so that a larger number of different tiles with the same number of pips are available.

table 10A	image	symbol	category
		5-5-5	triple all are the same
		6-6-0	left double the left and middle cells are the same
		4-1-4	outside double both ends are the same
		3-1-1	right double the middle and right cells are the same
		2-3-1	single all are different

The symbol for each tile consists of the numbers, read left to right, when the long side of the tile is at the top.

Table 10B, similar to 2A, tells how many tiles are in each category of each size of set of triangular sesquidominoes.

table 10B	pip counts	number of tiles
		triples	left doubles	outside doubles	right doubles	singles	total
	0, 1, 2	3	6	6	6	6	27
	0, 1, 2, 3	4	12	12	12	24	64
	0…4	5	20	20	20	60	125
	0…5	6	30	30	30	120	216
	0…6	7	42	42	42	210	343
	0…n	n + 1	n × (n + 1)	n × (n + 1)	n × (n + 1)	(n − 1) × n × (n + 1)	(n + 1)3

Table 10C, which corresponds to 2B, is a complete triple-three set of 64 tiles.

table 10C	triples
	left doubles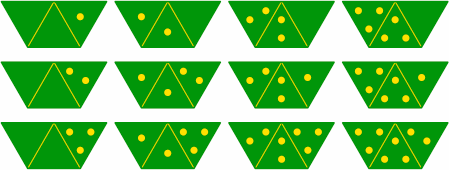
	outside doubles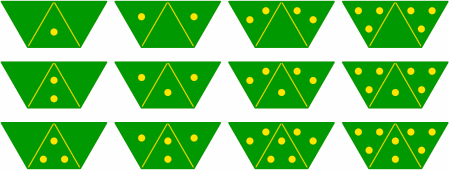
	right doubles
	singles

An obvious choice for playing surface is the regular hexagon, in whatever size players find best. Like figure 3A, figure 10D is half-scale.

figure 10D

§11. There are fifteen ways to fit two tiles together. Twelve of them form six mirror-image pairs, and they are illustrated in the upper compartment of figure 11A. Three non-pairing fittings are in the lower compartment. In every case, one the tiles is 1-2-3 or 3-2-1.

figure 11A

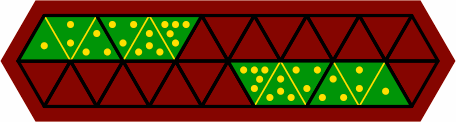
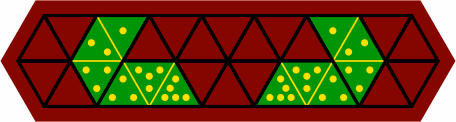
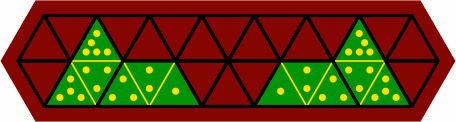
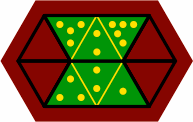
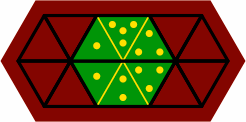
Figure 11B is a rather dense layout example. Although the saturation rule of §5 has an equivalent for triangles, it is not enforced here. Note also that cornerwise-adjacent cells frequently do not bear the same number.

figure 11B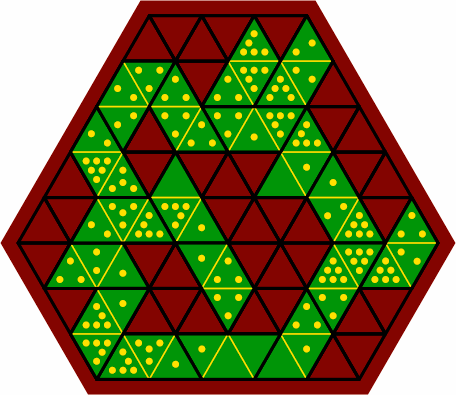

§12. While the three-triangle sesquidominoes may be whatever size is convenient, players might prefer something coordinated with the three-square version. For instance, if the three-square tiles are 25mm by 75mm, then the three-triangle tiles would have a short edge of 25mm and a long edge of 50mm. With that, the squares and triangles would abut cleanly, offering great variety in game play.

A complication of using the two shapes together is that, because the square root of three is irrational, a playing surface (analogous to figure 3A or 10D) cannot be marked with alignments for all possible layouts, as they are infinitely dense. As a consequence, players might choose a layout grid that permits only a subset of possibilities, or might elect to dispense with a grid entirely. Without any kind of grid, however, a difficulty arises in ensuring that tiles are placed accurately. This problem becomes salient when a large loop is attempted and needs to be verified.

The figures were prepared with Adobe PostScript.