The deltoidal hexecontahedron (plural -hedra) is covered by Wikipedia, MathWorld and others. Sometimes the figure is called strombic rather than deltoidal, and hexecontahedron is also spelled hexacontahedron.

In the discussion we save space by writing ico to mean a regular icosahedron, dod for a regular dodecahedron, and hex for a deltoidal hexecontahedron. Similarly, im (for ico magnitude) represents the distance from the center of an ico to each of its vertices, while dm serves the same role for the dod.

This page is offered because many sources give the impression that there is only one hex, when in fact there is a whole family of them, parameterized by a real number; the rhombic hexecontahedron thence becomes incorporated as a special case. This page examines the family's geometry in detail.

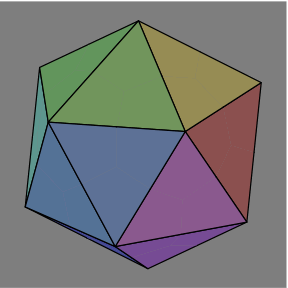
Here is one method of constructing the hexes. Beginning with a ico (figure 1A), partition each face (figure 1B) by drawing line segments (shown in white) from the center of each face to the centers of the face's edges.

1A

1B

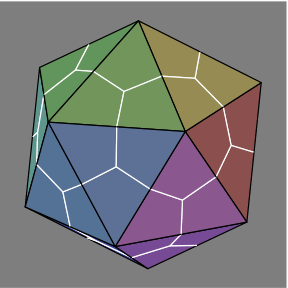
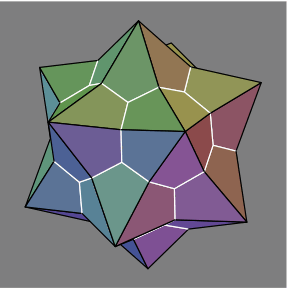
Each triangle is now three kites, and the points where three white lines intersect are the vertices of a dod, concentric with the ico. Now move each dod vertex closer to (figures 1C and 1D) or farther from (1E and 1F) the center. All of the dod vertices should be moved the same distance.

1C	1D
1E	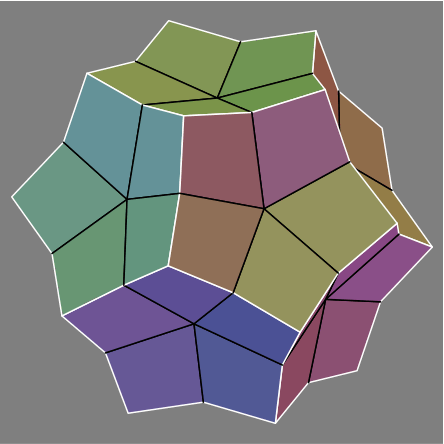1F

Throughout figures 1A-1F, the ico vertices (the points where five black lines meet) do not move. Meanwhile, the 20 dod vertices (three white lines) all move by the same arbitrary amount. What about the 30 other vertices, where a black line meets a white line?

The position of each is unique once im and dm are chosen. Although their calculation will be addressed later, we can mention now that these 30 vertices are the corners of a icosidodecahedron, which name is here written briefly as rec because the shape arises from rectifying either an ico or dod. The rec is concentric with the ico and dod, and we write rm for the distance from each rec vertex to the center. The rec will be illustrated later.

A second method of constructing the hexes arises from duality. It begins with a dod (figure 2A), each face partitioned into five kites (figure 2B) by drawing line segments (shown in black) from the center of each face to the centers of the face's edges.

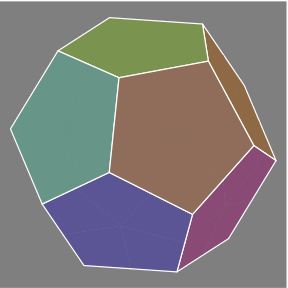2A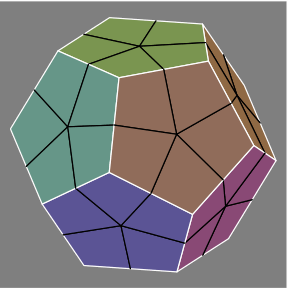

2B

Much as before, move each ico vertex closer to (figures 2C and 2D), or farther from (figures 2E and 2F), the center of the figure.

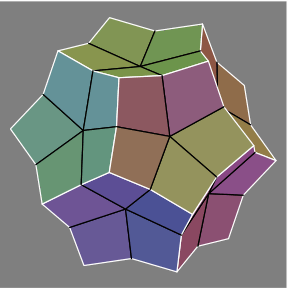2C	2D
2E same as 1E	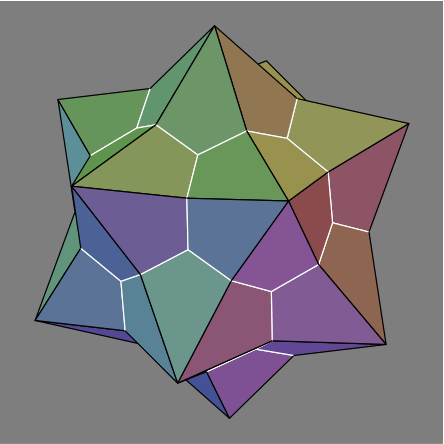2F

Among these six figures 2A-2F, the dod vertices, where three white lines meet, do not move.

Figures 3A through 3D show how an rec, rendered with dotted edges in figures 3C and 3D, fits within the hex.

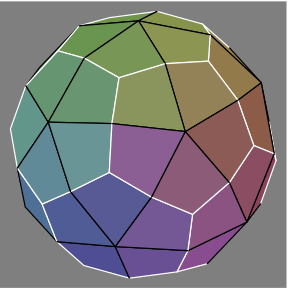3A same as 1E	3B
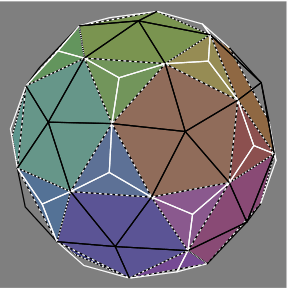3C	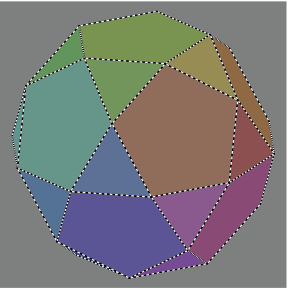3D

Evident is that some hexes could be constructed by erecting suitable pyramids on the rec. Other hexes would also require removal of pyramidal regions.

Two numbers that will be important in the subsequent calculations are:

• φ = 0.5 × (1.0 + √5)) = 1.618034
• κ = √(6 + 3 × φ) ÷ (φ + 1) = 1.258409

Although im and dm can be chosen arbitrarily, their ratio is the parameter of a family of hexes. Here are the principal cases, where ρ = dm ÷ im:

• When ρ < κ⁻¹,
  • Vertices at the intersection of three edges will be concave.
  • Vertices at the intersection of four edges will be saddle-shaped.
  • Vertices at the intersection of five edges will be convex.
• When ρ = κ⁻¹, the hex will be congruent to an ico. Since adjacent faces are coplanar, this polyhedron is improper.
• When κ⁻¹ < ρ < κ⁺¹, the hex will be convex. Arguably the best approximation to a sphere occurs when ρ = κ⁰ = 1.
• When ρ = κ⁺¹, the hex will be congruent to a dod. This polyhedron is also improper.
• When ρ > κ⁺¹,
  • Vertices at the intersection of three edges will be convex.
  • Vertices at the intersection of four edges will be saddle-shaped.
  • Vertices at the intersection of five edges will be concave.

These are enough numbers to appreciate the images in the next section; detailed calculations will come after that.

Below is a gallery of hexes, some of which have appeared above. To obtain images of roughly equal size, the following scaling convention has been adopted:

• Among the hexes where ρ equals κ raised to a nonpositive power, all ico vertices (five black lines) are fixed.
• Among the hexes where ρ equals κ raised to a nonnegative power, all dod vertices (three white lines) are fixed.

ρ = κ−13	ρ = κ−8	ρ = κ−5
ρ = κ−3	ρ = κ−2	ρ = κ−1
ρ = κ−0.5	ρ = κ0	ρ = κ+0.5
ρ = κ+1	ρ = κ+2	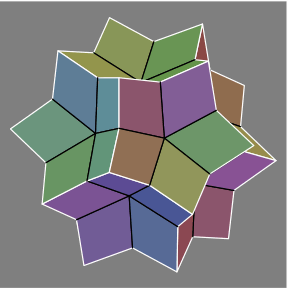ρ = κ+3
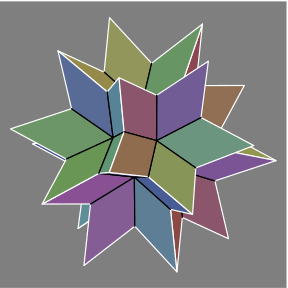ρ = κ+5	ρ = κ+8	ρ = κ+13

The faces are rhombi when ρ = (φ * √3) ÷ √(3 − φ) = 2.383963 = κ^+3.779736

same as 1B

Here is more detail about how the hexes were constructed for the images. First we adopted the following twelve values, in cartesian coordinates, as the vertices of the ico in figure 1B:

• (0, ±1, ±φ)
• (±1, ±φ, 0)
• (±φ, 0, ±1)

If we multiply dm by a factor f, we have to multiply rm by the factor g = (4 × f ) ÷ (3 + f ) to ensure that all four vertices of each kite remain coplanar, and that all kites remain congruent. For simplicity, im was kept constant.

Let

• a = φ + 2
• b = g × φ
• c = f ² × φ⁴ ÷ 3
• d = f × φ³ ÷ 3

• The length of a black edge is √(a + b² − 2 × φ × b)
• The length of a white edge is √(c + b² − 2 × b × d)
• The length of the major diagonal of a kite (iso vertex to dod vertex) is √(a + c − 2 × φ × d)

With one diagonal and all four sides of each kite established, it is easy to calculate the other diagonal, the angles, and the area.

Should we decide to change im, we need to adjust dm and rm proportionately.

Although this scheme begins with the ρ = κ⁻¹ case, the alternative starting with ρ = κ⁺¹ (as suggested in figures 2A-2F) would have given equivalent results, because of duality.