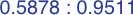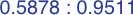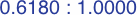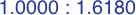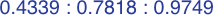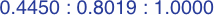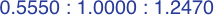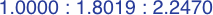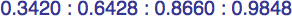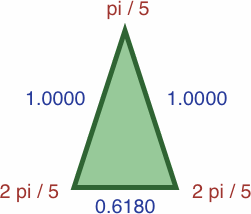
First we develop the golden ratio using angles that are multiples of π / 5 = 36 degrees. It is convenient to define:

• a = sin (π / 5) = sin (4 π / 5) ≈ 0.58778525
• b = sin (2 π / 5) = sin (3 π / 5) ≈ 0.95105652

Beyond those relations, a / b = 2 cos (2 π / 5) and b / a = 2 cos (π / 5); for another use of these numbers see quintrights.

Students of aesthetics often regard a rectangle as elegant if its width and height are in the ratio b : a.

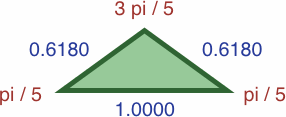
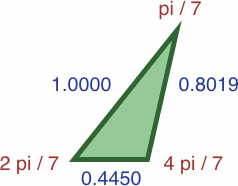
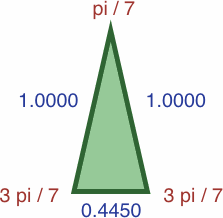
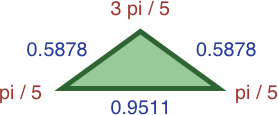
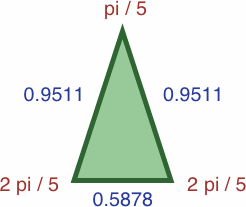
We can draw certain triangles where the length of each side is precisely the sine of the opposite angle; in the images we write four-place approximations to reduce bulk:

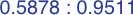
#5A	area = a2b / 2 ≈ 0.16429097	#5B	area = ab2 / 2 ≈ 0.26582838

Conveniently, the area of each triangle is half the product of its sides. This is true for any triangle where the length of each side is equal to the sine of the opposite angle.

Only one tetrahedron can be built from any combination of the two triangles above; it is a disphenoid which uses four instances of triangle #5B, and has a volume of √(4a⁴b² − 2a⁶) / 12 ≈ 0.04925738.

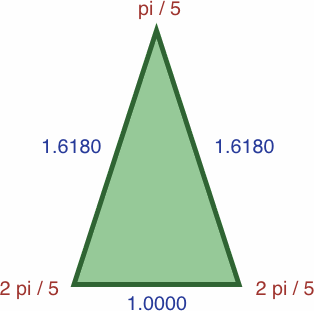
Proportionally enlarging the triangles gives unity and the golden mean:

#5A	#5B

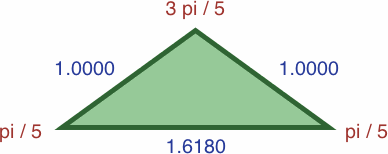
Further enlargement yields unity and the golden ratio:

#5A	#5B

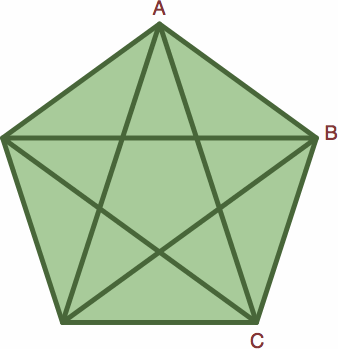
The figure below is a regular pentagon drawn with all its diagonals, but not to the same scale as any figure above. If the length of AB equals 0.5878, then AC ≈ 0.9511.

We can write sequences of powers of two ratios as in the table below wherein appears the Fibonacci sequence:

(a/b)−5 = +8 + 5 (a/b) ≈ 11.090170 (a/b)−4 = +5 + 3 (a/b) ≈ 6.854102 (a/b)−3 = +3 + 2 (a/b) ≈ 4.236068 (a/b)−2 = +2 + 1 (a/b) ≈ 2.618034 (a/b)−1 = +1 + 1 (a/b) ≈ 1.618034 (a/b) 0 = +1 + 0 (a/b) ≈ 1.000000 (a/b)+1 = 0 + 1 (a/b) ≈ 0.618034 (a/b)+2 = +1 − 1 (a/b) ≈ 0.381966 (a/b)+3 = −1 + 2 (a/b) ≈ 0.236068 (a/b)+4 = +2 − 3 (a/b) ≈ 0.145898 (a/b)+5 = −3 + 5 (a/b) ≈ 0.090170 (a/b) n = qn + rn (a/b) where: qn = qn−2 − qn−1 = rn−1 rn = rn−2 − rn−1 = qn−1 − rn−1

(b/a)−5 = −8 + 5 (b/a) ≈ 0.090170 (b/a)−4 = +5 − 3 (b/a) ≈ 0.145898 (b/a)−3 = −3 + 2 (b/a) ≈ 0.236068 (b/a)−2 = +2 − 1 (b/a) ≈ 0.381966 (b/a)−1 = −1 + 1 (b/a) ≈ 0.618034 (b/a) 0 = +1 + 0 (b/a) ≈ 1.000000 (b/a)+1 = 0 + 1 (b/a) ≈ 1.618034 (b/a)+2 = +1 + 1 (b/a) ≈ 2.618034 (b/a)+3 = +1 + 2 (b/a) ≈ 4.236068 (b/a)+4 = +2 + 3 (b/a) ≈ 6.854102 (b/a)+5 = +3 + 5 (b/a) ≈ 11.090170 (b/a) n = qn + rn (b/a) where: qn = qn−2 + qn−1 = rn−1 rn = rn−2 + rn−1 = qn−1 + rn−1

At the bottom of the table are recursive formulas to find higher powers. The formulas can be worked backwards to obtain lower powers.

Now we do a similar development using angles that are multiples of π / 7. In this case, it is convenient to write:

• a = sin (π / 7) = sin (6 π / 7) ≈ 0.43388374
• b = sin (2 π / 7) = sin (5 π / 7) ≈ 0.78183148
• c = sin (3 π / 7) = sin (4 π / 7) ≈ 0.97492791

Note that the golden counterpart in this π / 7 case will be a three-member ratio, such as a : b : c.

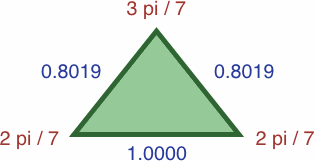
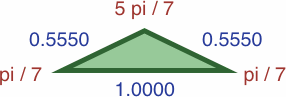
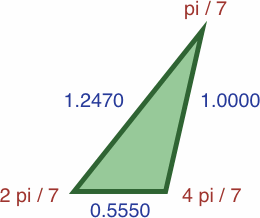
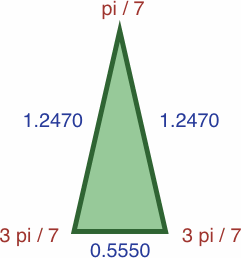
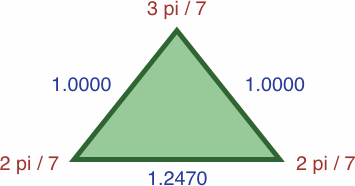
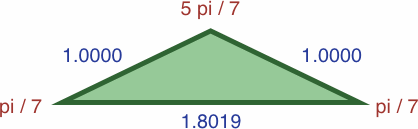
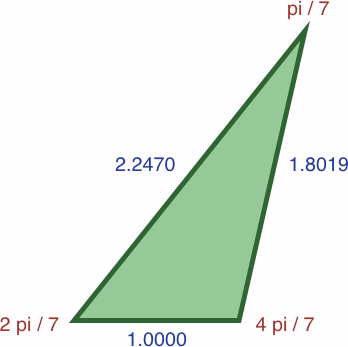
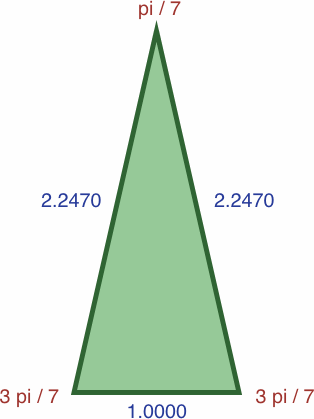
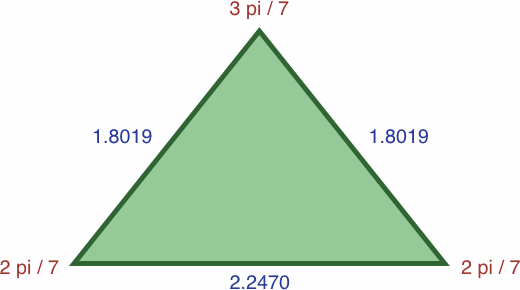
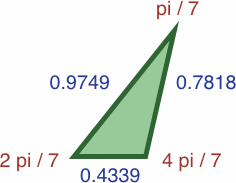
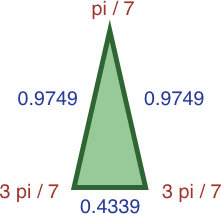
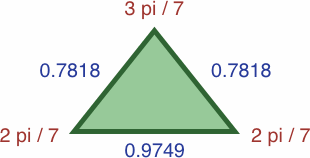
Here are four triangles where the length of each side is precisely the sine of the opposite angle:

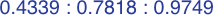
#7A	area = a2b / 2 ≈ 0.07359188	#7B	area = abc / 2 ≈ 0.16535946
#7C	area = ac2 / 2 ≈ 0.20619987	#7D	area = b2c / 2 ≈ 0.29796745

Two tetrahedra can be built from the triangles above, each a disphenoid:

• One uses four instances of triangle #7C, and has a volume of √(4a⁴c² − 2a⁶) / 12 ≈ 0.02903507.
• The other uses four instances of triangle #7D, and has a volume of √(4c⁴b² − 2c⁶) / 12 ≈ 0.05842414.

In each of the three following enlargements, the lengths have been scaled so that one value is equal to unity:

#7A	#7B
#7C	#7D

#7A	#7B
#7C	#7D

#7A	#7B
#7C	#7D

The figure below is a regular heptagon drawn with all its diagonals, but not to the same scale as any figure above. If the length of AB equals 0.4339, then AC ≈ 0.7818 and AD ≈ 0.9749.

Here are some powers of ratios:

(a/b)−5 = +14 + 14 (a/b) − 9 (a/b)2 ≈ 18.997607 (a/b)−4 = +9 + 5 (a/b) − 4 (a/b)2 ≈ 10.542877 (a/b)−3 = +4 + 5 (a/b) − 3 (a/b)2 ≈ 5.850855 (a/b)−2 = +3 + 1 (a/b) − 1 (a/b)2 ≈ 3.246980 (a/b)−1 = +1 + 2 (a/b) − 1 (a/b)2 ≈ 1.801938 (a/b) 0 = +1 + 0 (a/b) + 0 (a/b)2 ≈ 1.000000 (a/b)+1 = 0 + 1 (a/b) + 0 (a/b)2 ≈ 0.554958 (a/b)+2 = 0 + 0 (a/b) + 1 (a/b)2 ≈ 0.307979 (a/b)+3 = −1 + 1 (a/b) + 2 (a/b)2 ≈ 0.170915 (a/b)+4 = −2 + 1 (a/b) + 5 (a/b)2 ≈ 0.094851 (a/b)+5 = −5 + 3 (a/b) + 11 (a/b)2 ≈ 0.052638 (a/b) n = qn + rn (a/b) + sn (a/b)2 qn+1 = − sn rn+1 = qn + sn sn+1 = rn + 2sn	(b/a)−5 = +56 + 14 (b/a) − 25 (b/a)2 ≈ 0.052638 (b/a)−4 = +25 + 6 (b/a) − 11 (b/a)2 ≈ 0.094851 (b/a)−3 = +11 + 3 (b/a) − 5 (b/a)2 ≈ 0.170915 (b/a)−2 = +5 + 1 (b/a) − 2 (b/a)2 ≈ 0.307979 (b/a)−1 = +2 + 1 (b/a) − 1 (b/a)2 ≈ 0.554958 (b/a) 0 = +1 + 0 (b/a) + 0 (b/a)2 ≈ 1.000000 (b/a)+1 = 0 + 1 (b/a) + 0 (b/a)2 ≈ 1.801938 (b/a)+2 = 0 + 0 (b/a) + 1 (b/a)2 ≈ 3.246980 (b/a)+3 = −1 + 2 (b/a) + 1 (b/a)2 ≈ 5.850855 (b/a)+4 = −1 + 1 (b/a) + 3 (b/a)2 ≈ 10.542877 (b/a)+5 = −3 + 5 (b/a) + 4 (b/a)2 ≈ 18.997607 (b/a) n = qn + rn (b/a) + sn (b/a)2 qn+1 = − sn rn+1 = qn + 2sn sn+1 = rn + sn
(a/c)−5 = +56 + 14 (a/c) − 25 (a/c)2 ≈ 57.279030 (a/c)−4 = +25 + 6 (a/c) − 11 (a/c)2 ≈ 25.491566 (a/c)−3 = +11 + 3 (a/c) − 5 (a/c)2 ≈ 11.344814 (a/c)−2 = +5 + 1 (a/c) − 2 (a/c)2 ≈ 5.048917 (a/c)−1 = +2 + 1 (a/c) − 1 (a/c)2 ≈ 2.246980 (a/c) 0 = +1 + 0 (a/c) + 0 (a/c)2 ≈ 1.000000 (a/c)+1 = 0 + 1 (a/c) + 0 (a/c)2 ≈ 0.445042 (a/c)+2 = 0 + 0 (a/c) + 1 (a/c)2 ≈ 0.198062 (a/c)+3 = −1 + 2 (a/c) + 1 (a/c)2 ≈ 0.088146 (a/c)+4 = −1 + 1 (a/c) + 3 (a/c)2 ≈ 0.039229 (a/c)+5 = −3 + 5 (a/c) + 4 (a/c)2 ≈ 0.017458 (a/c) n = qn + rn (a/c) + sn (a/c)2 qn+1 = − sn rn+1 = qn + 2sn sn+1 = rn + sn	(c/a)−5 = +14 + 14 (c/a) − 9 (c/a)2 ≈ 0.017458 (c/a)−4 = +9 + 5 (c/a) − 4 (c/a)2 ≈ 0.039229 (c/a)−3 = +4 + 5 (c/a) − 3 (c/a)2 ≈ 0.088146 (c/a)−2 = +3 + 1 (c/a) − 1 (c/a)2 ≈ 0.198062 (c/a)−1 = +1 + 2 (c/a) − 1 (c/a)2 ≈ 0.445042 (c/a) 0 = +1 + 0 (c/a) + 0 (c/a)2 ≈ 1.000000 (c/a)+1 = 0 + 1 (c/a) + 0 (c/a)2 ≈ 2.246980 (c/a)+2 = 0 + 0 (c/a) + 1 (c/a)2 ≈ 5.048917 (c/a)+3 = −1 + 1 (c/a) + 2 (c/a)2 ≈ 11.344814 (c/a)+4 = −2 + 1 (c/a) + 5 (c/a)2 ≈ 25.491566 (c/a)+5 = −5 + 3 (c/a) + 11 (c/a)2 ≈ 57.279030 (c/a) n = qn + rn (c/a) + sn (c/a)2 qn+1 = − sn rn+1 = qn + sn sn+1 = rn + 2sn
(b/c)−5 = −14 + 14 (b/c) + 9 (b/c)2 ≈ 3.015065 (b/c)−4 = +9 − 5 (b/c) − 4 (b/c)2 ≈ 2.417895 (b/c)−3 = −4 + 5 (b/c) + 3 (b/c)2 ≈ 1.939001 (b/c)−2 = +3 − 1 (b/c) − 1 (b/c)2 ≈ 1.554958 (b/c)−1 = −1 + 2 (b/c) + 1 (b/c)2 ≈ 1.246980 (b/c) 0 = +1 + 0 (b/c) + 0 (b/c)2 ≈ 1.000000 (b/c)+1 = 0 + 1 (b/c) + 0 (b/c)2 ≈ 0.801938 (b/c)+2 = 0 + 0 (b/c) + 1 (b/c)2 ≈ 0.643104 (b/c)+3 = +1 + 1 (b/c) − 2 (b/c)2 ≈ 0.515729 (b/c)+4 = −2 − 1 (b/c) + 5 (b/c)2 ≈ 0.413583 (b/c)+5 = +5 + 3 (b/c) − 11 (b/c)2 ≈ 0.331668 (b/c) n = qn + rn (b/c) + sn (b/c)2 qn+1 = sn rn+1 = qn + sn sn+1 = rn − 2sn	(c/b)−5 = −56 + 14 (c/b) + 25 (c/b)2 ≈ 0.331668 (c/b)−4 = +25 − 6 (c/b) − 11 (c/b)2 ≈ 0.413583 (c/b)−3 = −11 + 3 (c/b) + 5 (c/b)2 ≈ 0.515729 (c/b)−2 = +5 − 1 (c/b) − 2 (c/b)2 ≈ 0.643104 (c/b)−1 = −2 + 1 (c/b) + 1 (c/b)2 ≈ 0.801938 (c/b) 0 = +1 + 0 (c/b) + 0 (c/b)2 ≈ 1.000000 (c/b)+1 = 0 + 1 (c/b) + 0 (c/b)2 ≈ 1.246980 (c/b)+2 = 0 + 0 (c/b) + 1 (c/b)2 ≈ 1.554958 (c/b)+3 = +1 + 2 (c/b) − 1 (c/b)2 ≈ 1.939001 (c/b)+4 = −1 − 1 (c/b) + 3 (c/b)2 ≈ 2.417895 (c/b)+5 = +3 + 5 (c/b) − 4 (c/b)2 ≈ 3.015065 (c/b) n = qn + rn (c/b) + sn (c/b)2 qn+1 = sn rn+1 = qn + 2sn sn+1 = rn − sn

Sequences of integers from the table above, namely:

… +155, +89, +47, +28, +14, +9, +4, +3, +1, +1, 0, 0, −1, −2, −5, −11, −25, −56, −126, −283, −636 … … +131, +66, +42, +19, +14, +5, +5, +1, +2, 0, +1, 0, +1, +1, +3, +6, +14, +31, +70, +157, +353 … increasing i → recursion formula: xi = + 2xi−1 + xi−2 − xi−3

… −155, +89, −47, +28, −14, +9, −4, +3, −1, +1, 0, 0, +1, −2, +5, −11, +25, −56, +126, −283, +636 … … +131, −66, +42, −19, +14, −5, +5, −1, +2, 0, +1, 0, +1, −1, +3, −6, +14, −31, +70, −157, +353 … increasing i → recursion formula: xi = − 2xi−1 + xi−2 + xi−3

are generalizations of the Fibonacci sequence. See these links:

• 1, 1, 3, 4, 9, 14
• 1, 2, 5, 11, 25, 56
• 2, 1, 5, 5, 14, 19
• 1, 1, 3, 6, 14, 31

As i increases without bound in the above sequences, x_i+1 / x_i approaches, depending on the sequence, one of these values:

• + sin (3 π / 5) / sin (π / 5) = +c/a, or
• − sin (3 π / 5) / sin (π / 5) = −c/a.

On the other hand, as i decreases without bound, x_i−1 / x_i approaches ±b/a.

In the standard Fibonacci sequence, the limiting ratio of consecutive terms is one of the following values, depending on whether the sequence is reckoned forward or backward:

• + sin (2 π / 5) / sin (π / 5), or
• − sin (2 π / 5) / sin (π / 5).

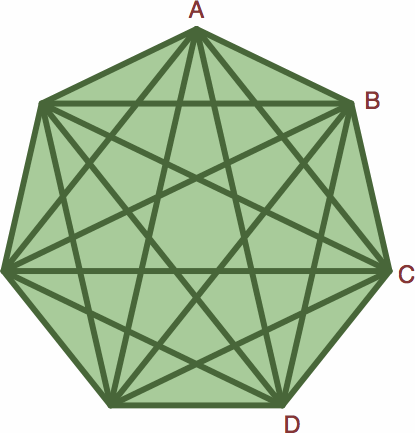
Everything readily extends to π / n where n is an odd number. In the π / 9 case:

• a = sin (π / 9) = sin (8 π / 9) ≈ 0.34202014
• b = sin (2 π / 9) = sin (7 π / 9) ≈ 0.64278761
• c = sin (3 π / 9) = sin (6 π / 9) ≈ 0.86602540
• d = sin (4 π / 9) = sin (5 π / 9) ≈ 0.98480775

The native four-member ratio is:

• 0.3420 : 0.6428 : 0.8660 : 0.9848

• 0.3473 : 0.6527 : 0.8794 : 1.0000
• 0.3949 : 0.7422 : 1.0000 : 1.1372
• 0.5321 : 1.0000 : 1.3473 : 1.5321
• 1.0000 : 1.8794 : 2.5321 : 2.8794

Also, cos (π / 9) × cos (2 π / 9) × cos (3 π / 9) × cos (4 π / 9) = 1 / 16.

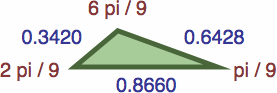
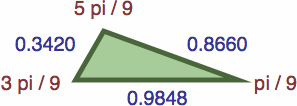
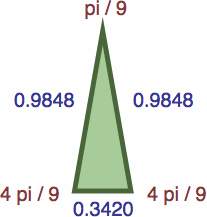
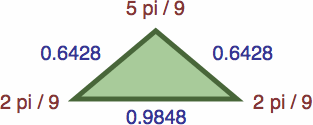
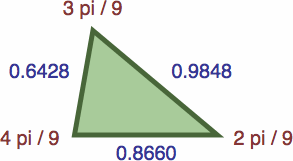
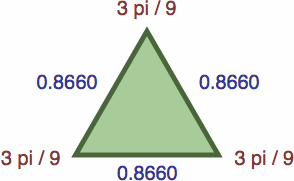
Following are seven triangles where the length of each side is precisely the sine of the opposite angle; their enlargments are omitted to save space.

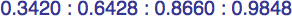
#9A	area = a2b / 2 ≈ 0.03759593	#9B	area = abc / 2 ≈ 0.09519624
#9C	area = acd / 2 ≈ 0.14584911	#9D	area = ad2 / 2 ≈ 0.16585349
#9E	area = b2d / 2 ≈ 0.20344942	#9F	area = bcd / 2 ≈ 0.27410666
#9G	area = c3 / 2 ≈ 0.32475953

Tetrahedra can be made from:

• four instances of #9D
• four instances of #9F
• four instances of #9G

In the general π / n case, if n is not only an odd number but also a multiple of three, one of the triangles will be equilateral.