Related is the same author's examination of a similar matter, emphasizing the algebraic aspects. This page by contrast emphasizes the artistic possibilities.

A polygon is equiangular (or isogonal) if all its angles are equal, and equilateral if all its sides are equal. A polygon might satisfy either criterion or neither, but a polygon that satisfies both is regular.

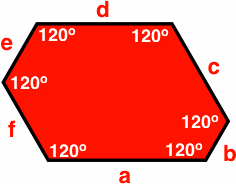
This report looks at equiangular hexagons, particularly with respect to the patterns that can be achieved with paving bricks and flooring tiles. With equiangularity each of the six angles must be 120 degrees. Because opposite sides are parallel, such a figure qualifies as a generalized parallelogram. We use the letter a to designate the bottom edge of the hexagon, or the length of that edge. Proceeding counterclockwise, the remaining sides are b, c, d, e and f.

The lengths of the six sides cannot be chosen freely, as a triple constraint follows from equiangularity:

• a + b = d + e
• b + c = e + f
• c + d = f + a

The lengths of a, b and c can be selected from the positive numbers without restriction; then d must lie between two extremes:

• d > a − c
• d < a + b

Once d is selected, e and f are completely determined:

• e = a + b − d
• f = c + d − a

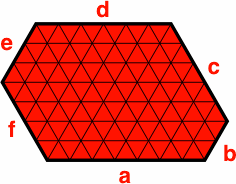
For convenience, we restrict the length of sides of hexagons to be in the ratio of small positive integers; this eases the description with no loss of generality. It also allows us to draw equilateral triangles within the hexagon that make it easier to see how long each side is; a formula for the quantity of triangles is (a + b + c)² − a² − c² − e².

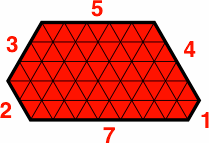
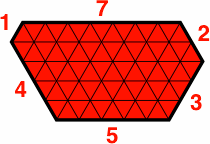
Because single-digit integers are sufficient for a variety of examples, a complete description of a hexagon can be given in a compact notation. For instance, the symbol H714532 stands for the hexagon (as pictured below) whose bottom side a is 7 units long, with side b = 1 unit, c = 4, d = 5, e = 3 and f = 2. This notation specifies not only the sequence of sides of a hexagon, but also its orientation. If this figure were rotated 180 degrees, the symbol would become H532714. When the rotation does not matter, as in a listing of possible tiles, it is reasonable to regard the hexagon as rotated so that the smallest number appears first, thus H145327.

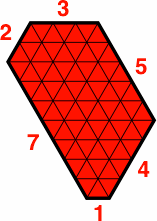H714532	H532714	H145327

Because e and f are determined by the other four sides, Habcd is unambiguous. For instance, H7145 must be the same as H714532. Further abbreviations are defined for the periodic hexagons:

• Habc = Habcabc; example H254 = H254254
• Hab = Hababab; example H37 = H373737
• Ha = Haaaaaa; example H1 = H111111

A few examples of aperiodic hexagons are listed below. Some have an axis of symmetry, denoted by the letter s.

H122213 s H123214 s H124215 s H125216 s H126217 s

H134316 s H135226 H135317 s H136227 H142324 s

H144326 H144417 s H145236 H145327 H146237

H154245 s H154336 H154427 H155246 H155337

H164346 s H164437 H165256 s H165347 H166257

In principle, a side of length zero is possible, but it will be rejected here because it does not add to the theory, and because the acute angle that results invites mistakes in assembling the patterns discussed later. Another reason for exclusion is that paving bricks and flooring tiles are often made of brittle materials, and the projections formed by an acute angle have a tendency to crack. In the figure below, b = 0.

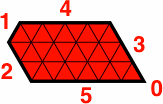H503412

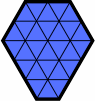
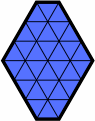
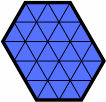
The hexagons in the next table will suffice for many purposes. Included are all figures where no side is longer than three units; if no side is longer than two, it is rendered in green.

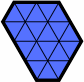
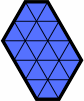
H1	H112	H113	H12
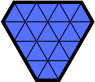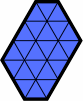
H122	H122213	H123	H13
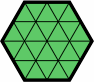H132	H132223	H133	H2
H223	H23	H233	H3

The plainest, and perhaps most common, tessellation of hexagons uses regular hexagons of uniform coloring, as below.

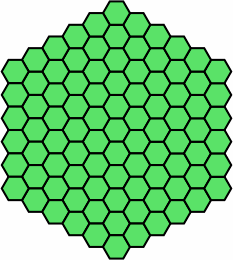
pattern 1

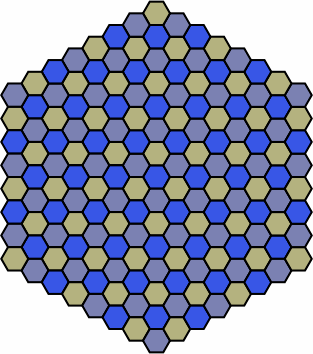
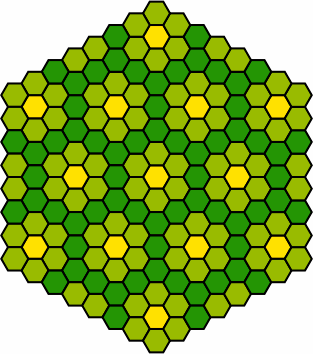
A common device is to vary the colors but not the shapes:

pattern 2	pattern 3

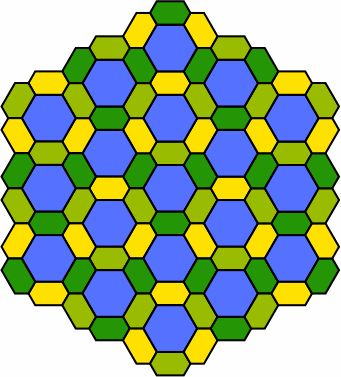
The patterns become more interesting when sizes and shapes are varied:

pattern 4

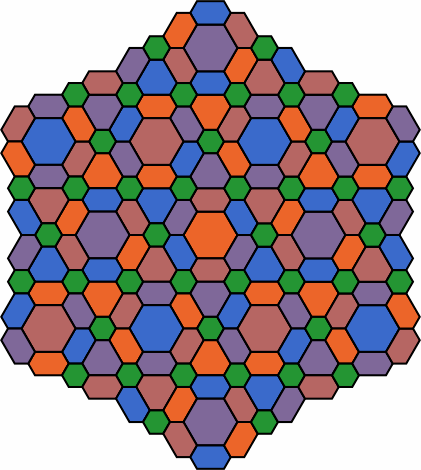
Pattern 5a, which uses H1, H12, H112 and H2, has mirror-image symmetry with respect to the shapes of the tiles but not their colors:

pattern 5a

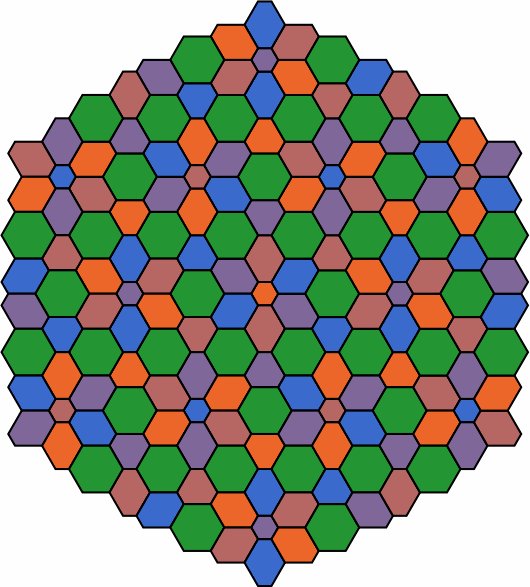
Pattern 5b is like 5a except that the long and short sides have been swapped:

pattern 5b

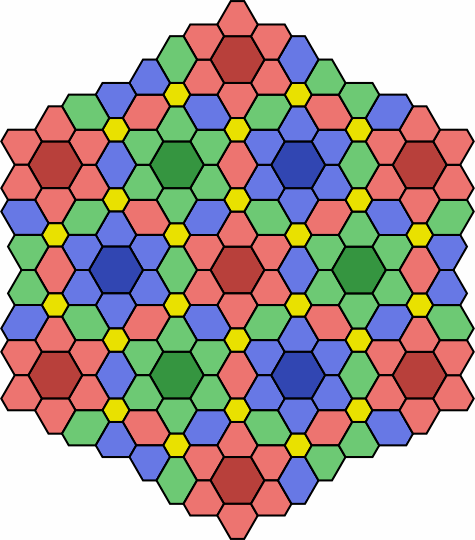
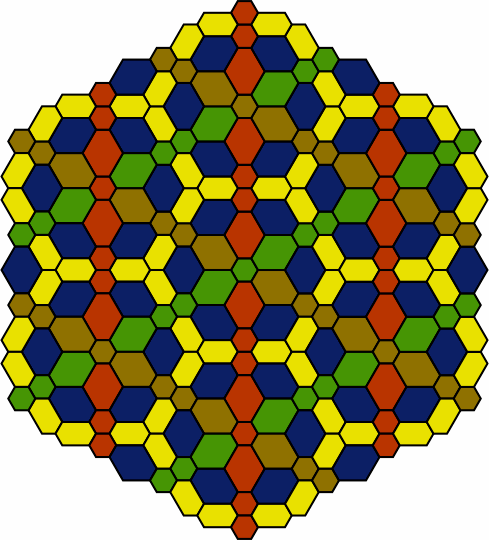
Adjoining tiles might sometimes be the same color, as in patterns 6 and 7. This is most effective when each cluster of homochromats remains small enough that individual tiles are readily discernable.

pattern 6

pattern 7

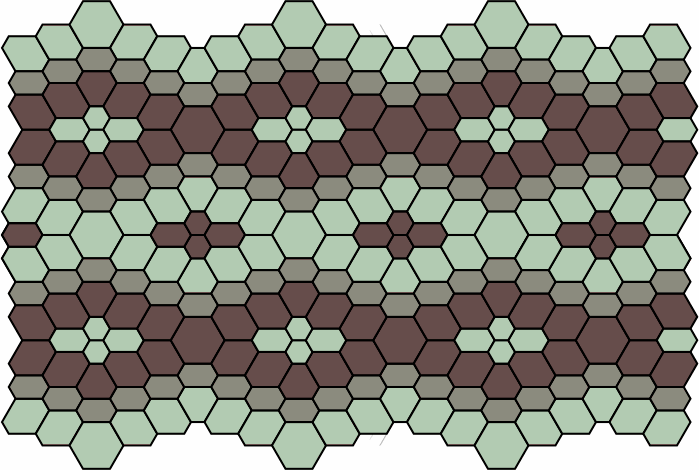
While the examples above are based upon a triangular tessellation, pattern 8 has the effect of stripes. This pattern benefits if the grout between tiles is in a color that contrasts with the tiles.

pattern 8