A problem with toy bricks,
– or –
A source of childhood frustration.
Version of Sunday 30 September 2012.
Dave Barber's other pages.
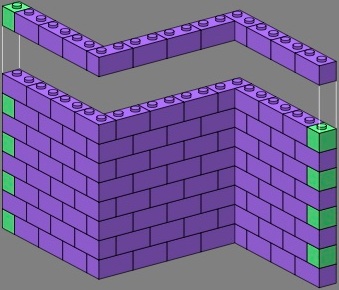
The simplest set of studded toy bricks contains pieces of two sizes, the single (on this page drawn in green for easy identification) and the double (in purple). Figure one is an example of a plain brick wall in stretcher bond which works satisfactorily with such pieces. The top course is lifted to give a better view of the second course.
| figure one |
|---|

|
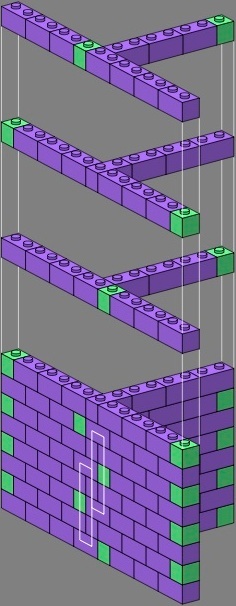
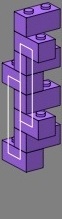
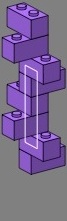
However, difficulties arise as soon as the juvenile builder tries a tee junction, and wants to solidly connect the two walls. Figure two shows one attempt, where three-course vertical joints (boxed in white) weaken the wall. Courses appear in cycles of four, but only three of them are different. Each smaller image on the right displays the core, consisting of the bricks immediately involved in the junction.
| figure two | figure three | |||
|---|---|---|---|---|
 | 
|  | 
| |
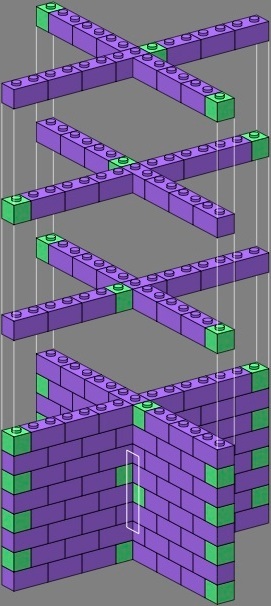
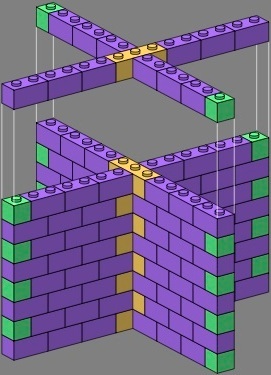
The crossing in figure three above fares no better, with three-course vertical joints in all four directions, one of them boxed in the drawing. This arrangement can be interpreted as having either four different courses, or one course rotated four different ways.
The same problem occurs with the typical brick that is used in real buildings. Like the double above it has a two-to-one length-to-width ratio, but in contrast it lacks the studs. Although the bricks supplied to a construction site are usually uniform in shape and size, masons frequently cut them to build a solid junction, to enable special bonding patterns, or to fit an irregular space. With real bricks, solidly-built tees and crosses almost always entail some cutting. On the other hand, parents routinely discourage their children from cutting their toy bricks.
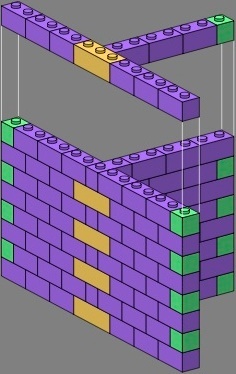
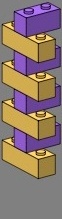
Figures four and five introduce triple bricks, rendered in gold, which are one way to make the multiple vertical joints unnecessary. Such triples have rarely been supplied by manufacturers, but would greatly aid the youthful bricklayer. A simplification also results, as there are now only two different courses in the tee and crossing:
| figure four | figure five | |||
|---|---|---|---|---|
 | 
|  | 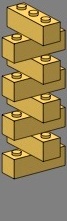
| |
Note that using a single or triple within a wall made primarily of doubles can disturb the phase, as highlighted by the white line in figure six:
| figure six |
|---|
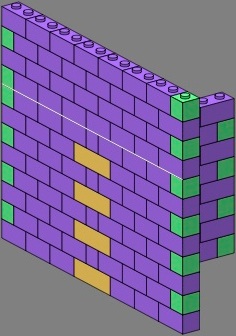
|
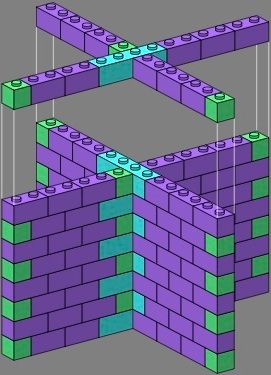
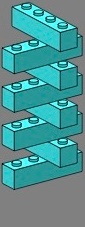
The quadruple brick, drawn below in cyan, preserves the phase of the bond through the tee or cross, even though this brick is placed asymmetrically relative to the junction:
| figure seven | figure eight | |||
|---|---|---|---|---|
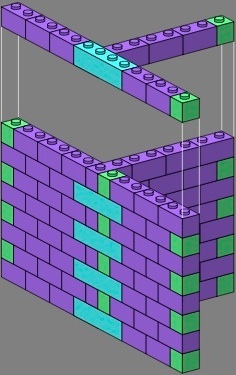 | 
|  | 
| |
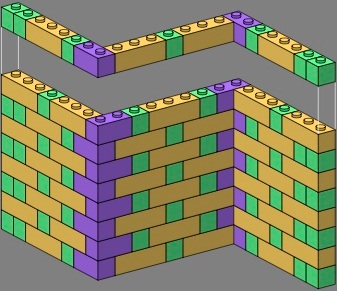
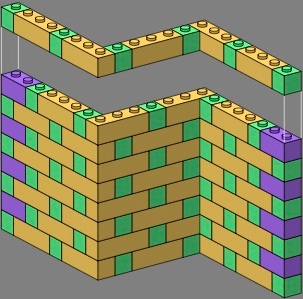
The triple brick also enables flemish bond. Here are two treatments of the ends and corners of a plain wall:
| figure nine | figure ten | |
|---|---|---|
| 
|
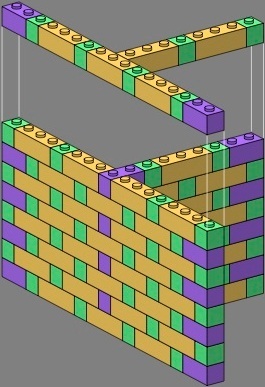
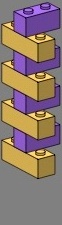
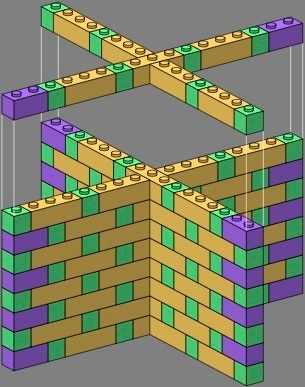
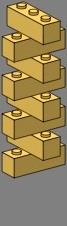
Next, flemish bond is applied to the tee and cross:
| figure eleven | figure twelve | |||
|---|---|---|---|---|
 | 
|  | 
| |
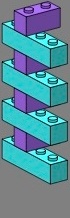
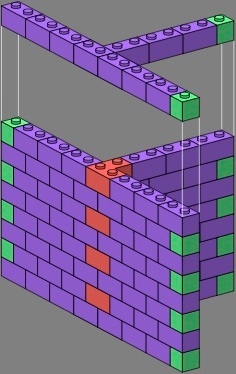
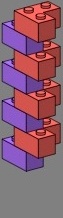
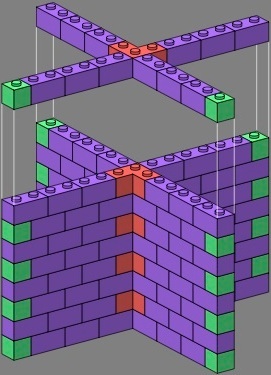
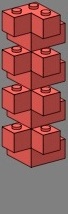
Right-angle triples (red) are another way to address the three-course vertical joint problem of figures two and three, and like the straight quadruples they preserve the phase of the doubles.
| figure thirteen | figure fourteen | |||
|---|---|---|---|---|
 | 
|  | 
| |
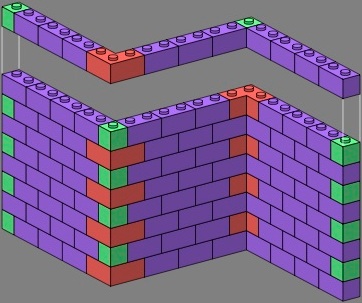
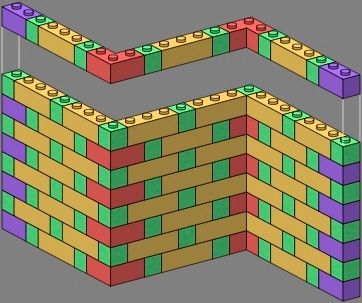
The right-angle bricks also can be used in a plain corner, whether stretcher bond or flemish:
| figure fifteen | figure sixteen | |
|---|---|---|
| 
|
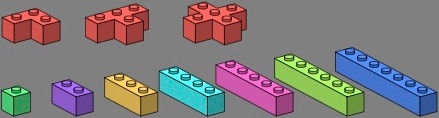
Figure seventeen is a recap of the one-wythe bricks seen so far, plus a few others. Depending on the production method, some manufacturers might find it unfeasible to make right-angle bricks. On the other hand, there should be little problem delivering straight bricks bearing five or more studs, which are useful in spanning gaps.
| figure seventeen |
|---|
|
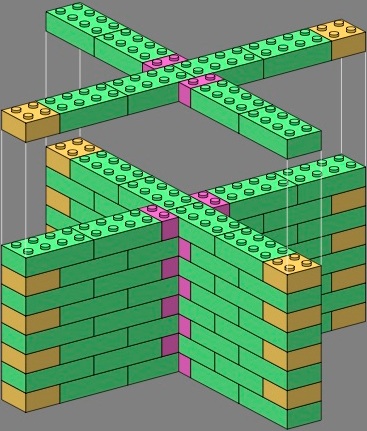
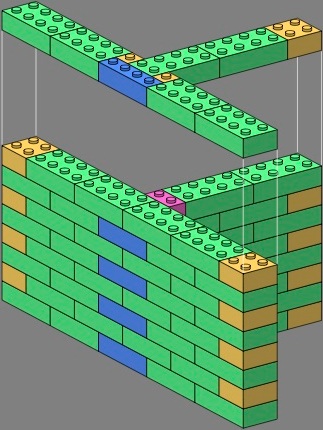
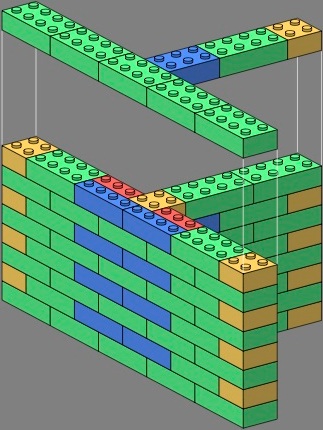
Two-wythe bricks offer more possibilities, particularly when combined with the one-wythes already established. Within each stright wall of each tee and crossing below, bricks remain in phase. The difference is how the phasing of one straight wall relates to the phasing of the perpendicular wall. The one-wythe bricks are especially helpful in giving the tees an attractive appearance.
In the following images, the bricks are rendered in a color scheme different from that above.
| figure eighteen | figure nineteen | |
|---|---|---|
| 
|
| figure twenty | figure twenty-one | |
|---|---|---|
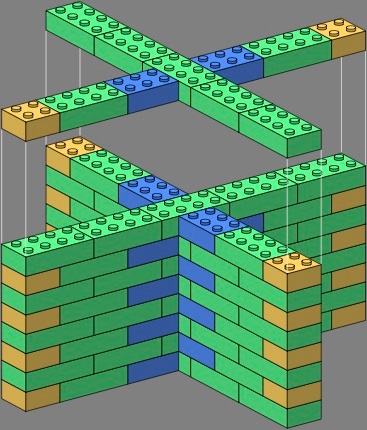
| 
|
| figure twenty-two |
|---|
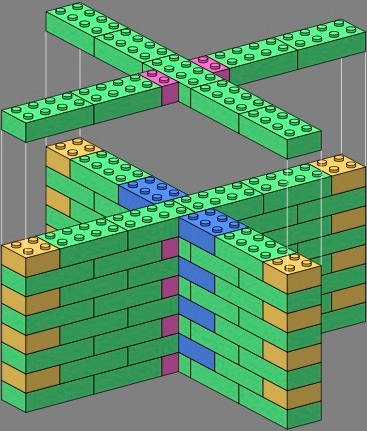
|
The figures were prepared with PostScript, which is Adobe's original product.