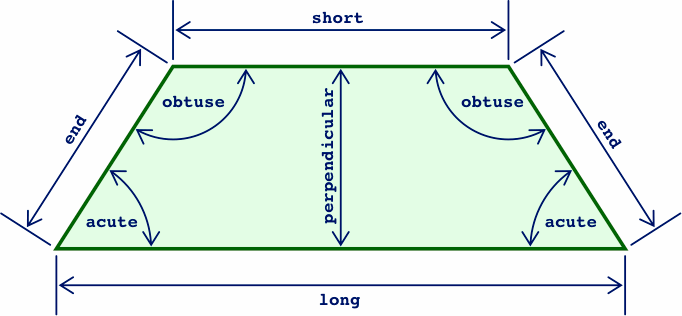
§1. Within the world of furniture for offices and schools, tables in the shape of a trapezoid have become more common in recent years.
The advantage of this shape is that several trapezoid tables (more briefly, traps) can be arranged adjacently, in many configurations, to give the effect of a larger table that fits into whatever space is available. Because typical traps are lightweight and are narrow enough to pass through ordinary doorways, they can easily be moved individually from one room to another as needs change.
However, people seeking to acquire them can find the selection of traps to be tricky because manufacturers in their catalogues are often not explicit about the exact sizes and shapes of their products. Many times only two distances are given, an ostensible length and width, and that is not enough to fully specify the table's size and shape. Of some mitigation is that virtually all traps are symmetrical, so that both ends are equal, both acute angles equal, and both obtuse angles equal.

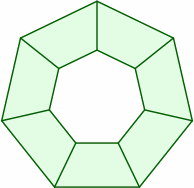
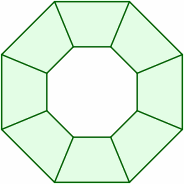
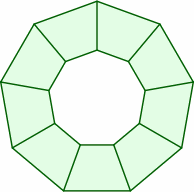
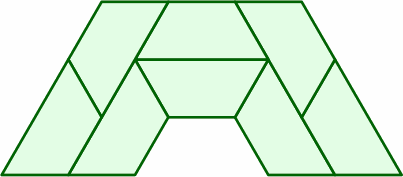
When two measurements are given for a trap, the larger almost always pertains to the long side, while the smaller number might plausibly represent either the end measurement or the perpendicular distance. Inconvenient is that many suppliers do not give a measurement for the short side or for the angles, but some sources do at least offer sample layout diagrams for multiple tables, and from those size information may be deduced. For instance, if eight traps are depicted in a uniform ring, there is a good chance that the acute angles are 67.5 degrees, and the obtuse 112.5. A few possibilities are shown below.
| uniform rings | ||
|---|---|---|
| 
| 
|
| acute = 45° obtuse = 135° | acute = 54° obtuse = 126° | acute = 60° obtuse = 120° |
| 
| 
|
| acute ≈ 64.3° obtuse ≈ 115.7° | acute = 67.5° obtuse = 112.5° | acute = 70° obtuse = 110° |
While this kind of ring is helpful in assessing the properties of a trap, the tables can, and usually will, be arranged in other ways.
§2. This report develops the particular trapezoid where:
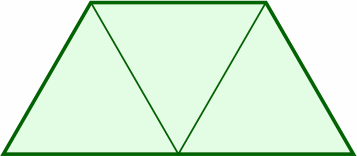
Six such traps form a uniform ring.
Certain details of table design are not developed in this report:
§3. No object can ever be built exactly to a specified size. Among other reasons, rulers and protractors invariably exhibit some inaccuracy, and materials will shrink and expand with changes in temperature and humidity. Thus a thorough approach includes a tolerance for each measurement of distance or angle.
For furniture, a tight tolerance is 2 percent of distance and 1 degree of angle; a loose tolerance is 6 percent of distance and 3 degrees of angle. Looser tolerances tend to reduce manufacturing costs, because cheaper tools and raw materials can be used, and workers of lower skill level can be employed. Also, fewer completed pieces have to be rejected for being out of specification. In the case of these traps, which are intended to be used in multiples, tighter tolerances become required if a mechanism is provided to latch abutting tables together.
Tables are often made of wood, and a complication arises in cutting that material: a kerf-width of the material is converted to sawdust. A typical kerf is on the order of 1/16 inch or 1.5 millimeters. Thus if a 12-inch board is cut in half, each resultant piece will be slightly less than 6 inches. In high-accuracy work, this must be taken into account.
Occasionally one will intentionally introduce a small error to squeeze a design onto standard-size raw materials, thereby reducing waste. Such an expedient is used in the scheme to follow.
§4. Popular for building furniture are sheets of plywood or particle board among the standard sizes of which are 48 × 96 inches, or the slightly smaller 1200 × 2400 millimeters. From one such sheet it is possible to cut four trap tops in a convenient size with minimal waste, and with few saw cuts, as explained below.
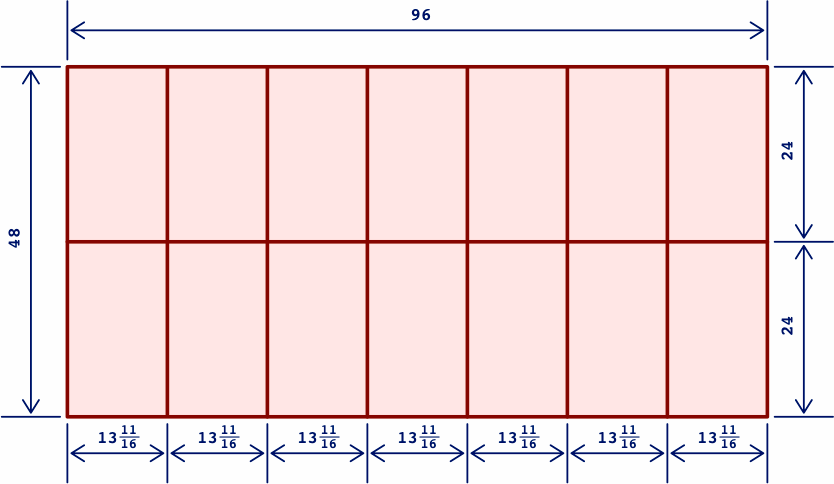
The first step is to draw reference lines om the sheet of wood dividing it into 14 equal rectangles. Here is the breakdown of the 48 × 96 board to the nearest sixteenth of an inch:
or the 1200 × 2400 board to the nearest millimeter:
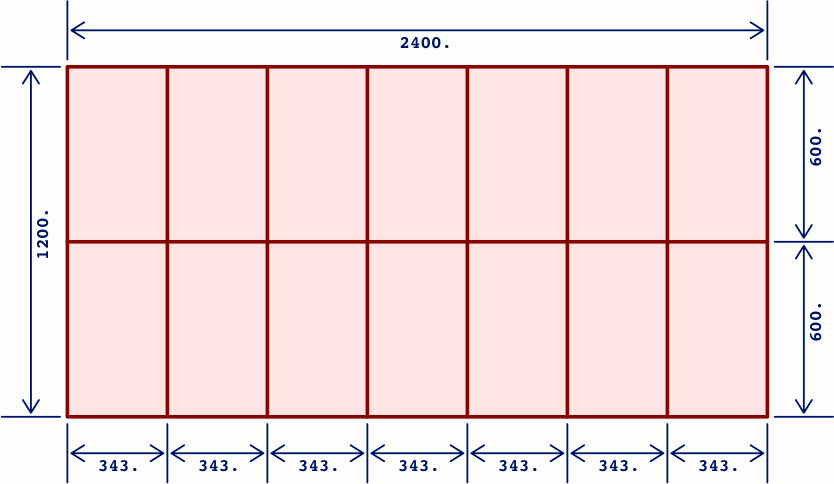
In these diagrams, inches are never written with a decimal point, but millimeters always have a point at the end; with that notational difference, a drawing can be dual-dimensioned without ambiguity. Although 96 inches is not exactly the same as 2400 millimeters, the two distances are close enough that the same drawing can be used to save space.
Diagonals such as the following complete the rudiments of layout. For angles, the decimal point will be written in the middle, so that degrees will not be confused with inches or millimeters:
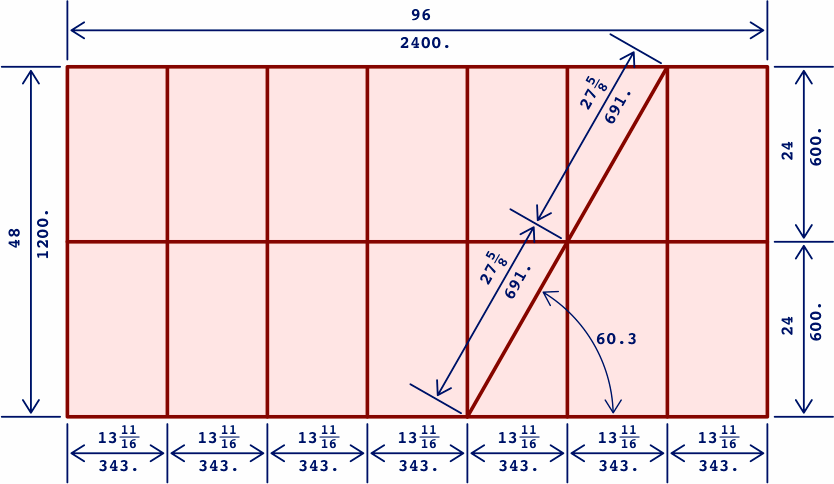
Many of these measurements are approximations; for instance the angle comes out to 60.3, not 60.0, degrees. Meanwhile, the diagonal distance 691 millimeters (27 + 5/8) is a little more than twice the horizontal distance of 343 (13 + 11/16) millimeters. Still, these distance errors are less than one percent, the angle error less than half a degree. To achieve significantly greater precision will require accounting for the kerf widths in the design process.
How long is a length unit? It varies slightly, according to whether millimeters or inches are used, and according to whether the measurement is taken parallel to the greater dimension of the uncut sheet of raw material, or oblique to it:
The variations arise from the minor inaccuracies that have been intentionally introduced, and will not affect table construction in most contexts. On the other hand, designers who seek the greatest precision will have to consider not only the kerf mentioned above, but also that many boards as supplied by the factory are slightly out of specification, either by being too large, too small, or out of square. Beyond that, sometimes a correctly-sized board has suffered dents on its edges during shipping and storage, so that its full extent is not usable. Even if perfectly constructed, adjoining tables will not align quite right if resting on an uneven floor.
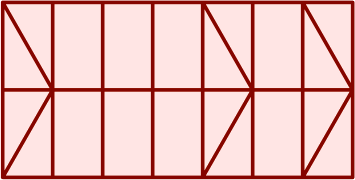
With the dimensions established, the cutting pattern follows without ado, and can be rendered at a smaller scale to save space. Draw these six diagonals:
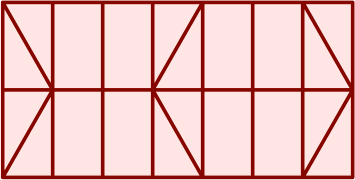
Then cut thus:
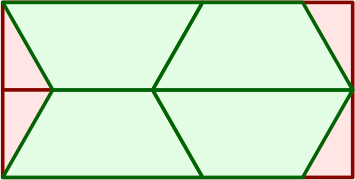
whence four traps:
Only seven cuts are required: one long cut along the middle of the board, producing two long rectangular planks; and then three oblique cuts in each plank. The four resultant traps are drawn here in green, while waste (amounting to about 14% of total board area) appears in red. If the raw material has a grain in the longitudinal direction, so will all four tables cut from it.
Without affecting overall functionality, the corners may be rounded to any desired radius or left sharp:


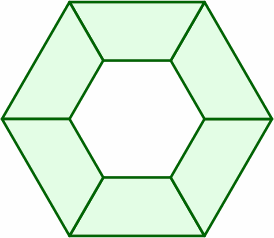
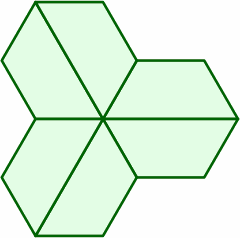
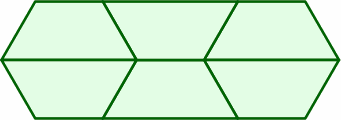
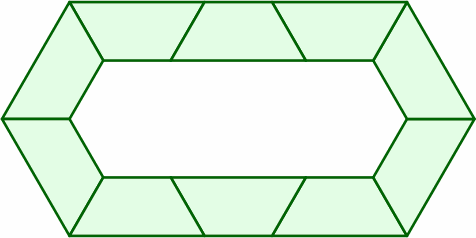
§5. A few of the many arrangements incorporating multiple tables are:
 | 
|
 | 
|
| |
| |
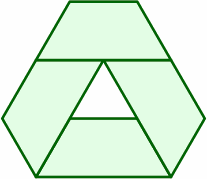
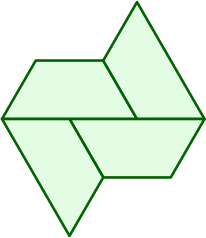
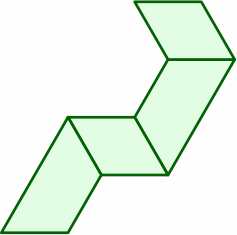
The following layouts succeed because the end and the short side are both 1 length unit, and the long side 2:
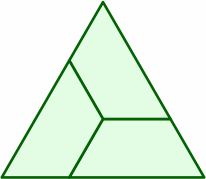 | 
|
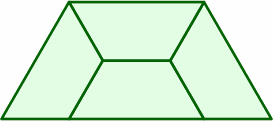 | 
|
| |
Also see canonical juxtapositions.
If an area unit is 205,800 = 600 × 343 square millimeters or 328.5 = 24 × (13 + 11/16) square inches, then the size of a trap is 3 area units.
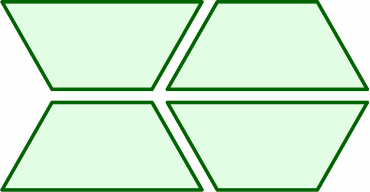
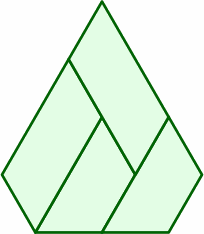
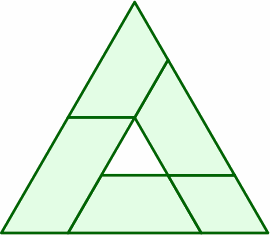
§6. A sheet might be divided into something other than four trapezoids:
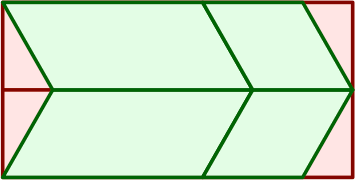
The parallelogram in the upper left is the mirror image of the parallelogram in the lower left, although if both faces of the board from which they are cut are of the same finish, this distinction may not matter during the manufacturing process. On the other hand, the two rhombi on the right are equal within the tolerances established above.
One can usually expect to get 12 total area units from a sheet of raw material, with 2 area units lost to waste.
 | 
|
 | 
|
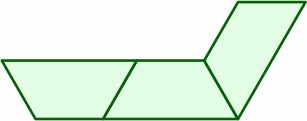
§7. Here is another cutting pattern:
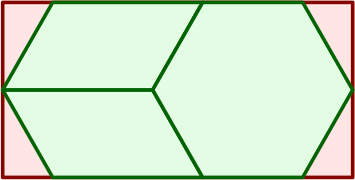
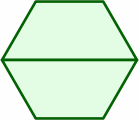
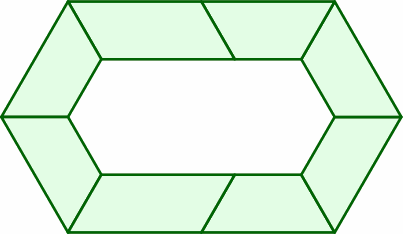
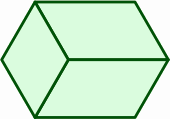
The hexagon at right is equivalent to two of the previously introduced traps back to back. Each side is one length unit.
The parallelograms are, as those above, mirror images of each other, but their size is now 3 area units. Each short side is 1 length unit, while each long side is 1.5 length units. Although a fraction, this latter number does not pose any problem in making tables line up neatly.
| |
| 
|
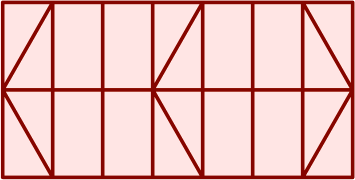
§8. A further cutting pattern is:
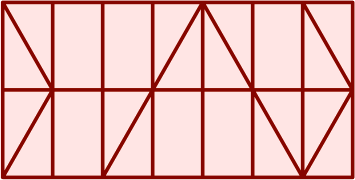
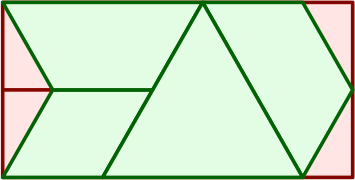
This affords a large triangle (4 area units), which might have one leg at each corner plus a fourth leg in the center if heavy loads are expected. Besides that are a rhombus and two traps. If the raw material has a longitudinal grain, one of the traps will carry its grain in a nonlongitudinal direction.
Colophon. The figures were generated with hand-coded Adobe PostScript, the superlative choice for images that are generated by calculation, while the HTML was prepared with an ordinary text editor. All the work was done on an iMac.