This is a detailed explanation of how the pips were designed, and how their sizes for the number cards were derived. Assumed is that all dimensions are in millimeters, and cards are 62.5 wide and 88.39 high.
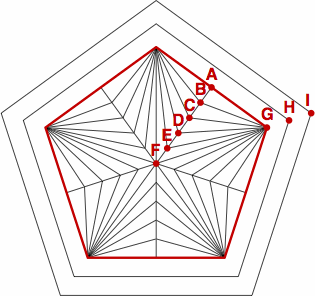
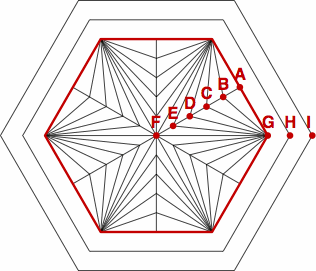
Each pip starts with a basic regular polygon, highlighted in red in figure X1 below. Point G is one corner of the basic polygon. Point A is the midpoint of one side, while point F is the center. Points B, C, D, and E are evenly spaced between A and F. Within any one pip, triangles GAB, GBC, GCD, GDE, and GEF all have the same area.
The H-F distance is 120% of the G-F distance, and the I-F distance is 140% of the G-F distance.
| figure X1 | 
| 
|
|---|
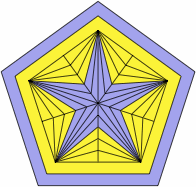
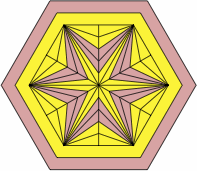
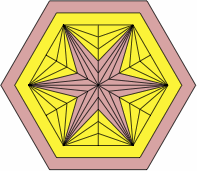
Then to produce the pips, selected areas are filled in:
| figure X2 | 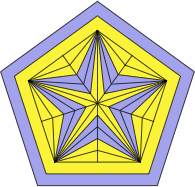
| 
| 
| 
|
|---|
The pip sizes for the number cards are in the table below. This diagram shows exactly what is being measured. Figure X3 is an excerpt from that diagram, for the 5-point pip that appears on a number card of rank 8:
| figure X3 | 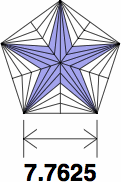
|
|---|
| suggested pip sizes for the number cards | |||||||
| s = number of sides | |||||||
|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | ||
| p = number of pips | 15 | 12.8137 | 8.4319 | 6.4284 | 5.2312 | 4.4232 | 3.8373 |
| 14 | 13.0817 | 8.6083 | 6.5628 | 5.3406 | 4.5157 | 3.9175< | |
| 13 | 13.3758 | 8.8018 | 6.7104 | 5.4607 | 4.6172 | 4.0056 | |
| 12 | 13.7009 | 9.0157 | 6.8734 | 5.5934 | 4.7295 | 4.1030 | |
| 11 | 14.0632 | 9.2541 | 7.0552 | 5.7413 | 4.8545 | 4.2115 | |
| 10 | 14.4712 | 9.5226 | 7.2599 | 5.9078 | 4.9954 | 4.3336 | |
| 9 | 14.9359 | 9.8284 | 7.4930 | 6.0975 | 5.1558 | 4.4728 | |
| 8 | 15.4731 | 10.1818 | 7.7625 | 6.3169 | 5.3412 | 4.6337 | |
| 7 | 16.1055 | 10.5980 | 8.0798 | 6.5750 | 5.5595 | 4.8230 | |
| 6 | 16.8678 | 11.0996 | 8.4622 | 6.8862 | 5.8227 | 5.0513 | |
| 5 | 17.8161 | 11.7236 | 8.9380 | 7.2734 | 6.1500 | 5.3353 | |
| 4 | 19.0496 | 12.5353 | 9.5568 | 7.7770 | 6.5758 | 5.7047 | |
| 3 | 20.7667 | 13.6652 | 10.4182 | 8.4780 | 7.1685 | 6.2189 | |
| 2 | 23.4528 | 15.4328 | 11.7658 | 9.5746 | 8.0958 | 7.0233 | |
| 1 | 28.8738 | 19.0000 | 14.4854 | 11.7877 | 9.9670 | 8.6467 | |
| general formula | 38.0 ×
exp
(−0.3 ×
log
(p)) ×
sqrt
(tan
(180° ÷ s) ÷ s)
The numbers 38.0 and −0.3 were arbitrarily chosen to give attractive results. | ||||||
Pip sizes for the ace cards are 15% smaller in linear measurement than their number-card equivalents, with A corresponding to 1, B to 2, et cetera. The smaller size allows room for the border. The number 15% was chosen arbitrarily.