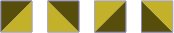
§1. About 300 years ago, Sebastien Truchet developed a geometric scheme, now known as Truchet tiles, for creating interesting patterns. Needed is a supply of identical square tiles: each is divided along a diagonal, yielding two right triangles to be rendered in different colors. The tiles, which can be rotated by any multiple of 90 degrees, are to be arranged in an ordinary square grid, either randomly or systematically to create attractive patterns.

Here are the four possible rotations of the original tile:

figure 1A

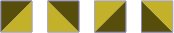
Figure 1B is a random placement of tiles:

figure 1B

Figure 1C is non-random:

figure 1C

§2. The popularity of Truchet tiles has increased greatly since the late-twentieth-century work of Cyril Smith. He used a simple modification, replacing the triangles with arcs (here called links) connecting the sides. In Smith's version, the sole tile has two distinct rotations:

figure 2A

Figure 2B is a random placement:

figure 2B

An option is to add a third tile with links that cross:

figure 2C

Figure 2D is a random placement with three kinds of tiles:

figure 2D

Statisticians have researched the distribution of the lengths and shapes of the paths in random placements; also worth examining is how paths can change when a subset of tiles are rotated. Others who have used this kind of tile are geometers and artists. Beyond that, game designers have employed Truchet tiles to advantage, often applying a coloring variant that results in two kinds of tiles, each with two distinct rotations:

figure 2E

Figure 2F displays these tiles in a distribution that is random, except that adjoining tiles are constrained to match in color:

figure 2F

A characteristic of this manner of coloration is that if the number of columns is even, then the right edge will match the left edge; similarly for the rows.

§3. Also in currency is an adaptation of Truchet tiles to regular hexagons. Figure 3A shows two different tiles, offering two or three rotations respectively:

figure 3A

Here is a random placement:

figure 3B

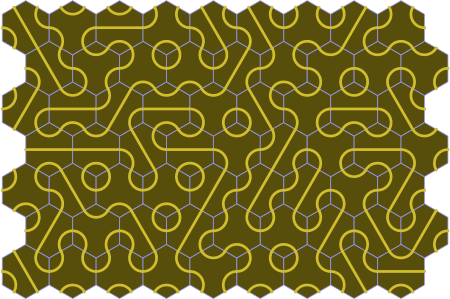
As with the square tiles, it is possible to have links that cross. The three tiles in figure 3C have three, six, and one rotation respectively.

figure 3C

Figure 3D is a random placement which includes cross-link tiles:

figure 3D

1. Each polygon has an even number of sides.
2. Each polygon is equilateral.
3. Each polygon is convex.
4. Each polygon is simple; in other words the boundary does not intersect itself.
5. Within a placement, all angles of all polygons are multiples of the chunk, which is a selected divisor of 180 degrees.
6. Opposite sides of a polygon are parallel. Opposite angles will thus be equal.

The properties were chosen to make tessellation relatively easy; an open question is whether the last property is merely a consequence of the others. In any case, each polygon (but not necessarily its link markings) has 180-degree rotational symmetry. Table 4A contains examples of chunk sizes:

table 4A
180° ÷ 2 = 90°	180° ÷ 6 = 30°	180° ÷ 10 = 18°
180° ÷ 3 = 60°	180° ÷ 7 ≈ 25.71°	180° ÷ 11 ≈ 16.36°
180° ÷ 4 = 45°	180° ÷ 8 = 22.5°	180° ÷ 12 = 15°
180° ÷ 5 = 36°	180° ÷ 9 = 20°	180° ÷ 13 ≈ 13.85°

A catalog gives many examples of suitable tiles; but as with most areas of mathematics, generalization along other avenues is possible. Indeed, there has been research in a three-dimensional counterpart.

Figure 4A is an example of placing tiles that have a chunk size of 36°; an important observation is that a placement need not be periodic. The dots represent the sizes of angles, as measured in chunks.

figure 4A — chunk 36°

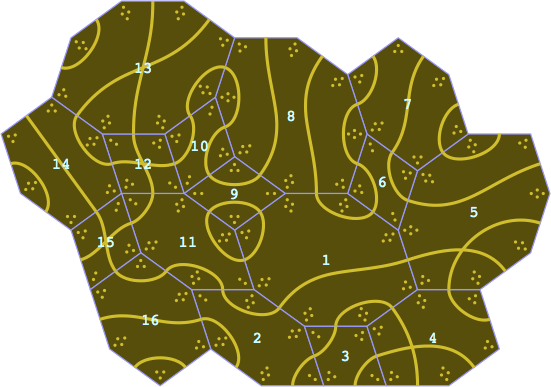
Figure 4B employs narrow tiles demonstrating how link curves might incidentally double-cross. Also revealed is how the angle dots, if drawn, might need to be situated outside the tile for lack of room.

figure 4B — chunk 36°

Colophon. This page was prepared on an Apple Macintosh running OS X. The html was written with an ordinary text editor, but the images were a little more complicated:

1. Images were generated by a C++ program under XCode.
2. Output from that program was itself a series of programs in the Abobe PostScript language.
3. The PostScript code was translated to pdf using pstopdf.
4. Each pdf file was converted to a gif file using Preview.
5. Minor editing of the gif files was done using GIMP.

The link curves in sections 2 and 3 are circular arcs. In section 4 they are instead cubic Bezier curves, because it is cumbersome to define a system of circular arcs to accommodate the irregular polygons.