Essential for playing at Bendominoes is proper alignment of the tiles — which are curved dominoes — as they are placed end to end. This report gives some examples of markings for a playing surface that will assist correct placement.

The set examined for this report has 28 tiles that correspond to traditional double-six dominoes:

figure 1	doubles
	non-doubles

The tiles of figure 1 can be characterized this way:

• All doubles
• Certain non-doubles:
  • Tiles with two even numbers, if the larger number is on the left
  • Tiles with two odd numbers, if the larger number is on the left
  • Tiles with one odd and one even number, if the larger number is on the right

One way to extend the set is to allow more than six pips; among traditional dominoes, double-nine and double-twelve sets are well known. Figure 2 illustrates another way to enlarge the set, with 21 non-double reverse tiles:

figure 2

Tiles have an outer radius of 33 millimeters, inner radius of 12 millimeters, and thickness of 10 millimeters. The exact distances are not critical as long as all tiles are the same size. Each curve subtends 120 degrees of arc, and this angle is critical so that three tiles precisely form a circle. The tiles might instead have been manufactured with a 90-degree angle, resulting in a similar game with four tiles forming a circle.

Pips come in a variety of colors as in figure 3, but for simplicity this report disregards that feature.

figure 3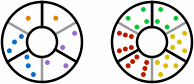

A convenient size of playing surface is this 24-disk board:

figure 4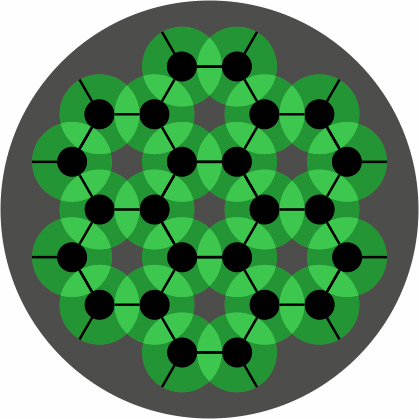

When a tile is placed on the board, its concave side should be touching a black dot, and both its ends should be touching black lines. Figure 5 shows the board with some correctly-placed tiles; no tile ever covers a gray region of the board.

figure 5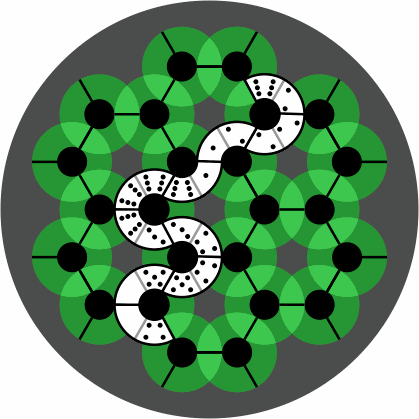

A 6-disk board, although not large enough for serious competition, has enough room to display the difference between wrong and right placement:

figure 6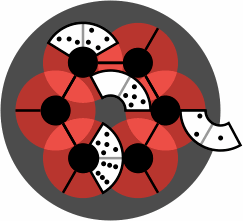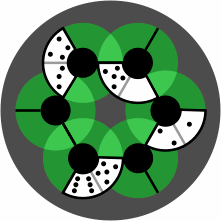
	wrong	right

In the usual rules for Bendomino games, each tile after the first must be placed end-to-end with a previous tile. However, this board allows the development of games and puzzles relaxing that rule, because proper alignment of tiles is assured.

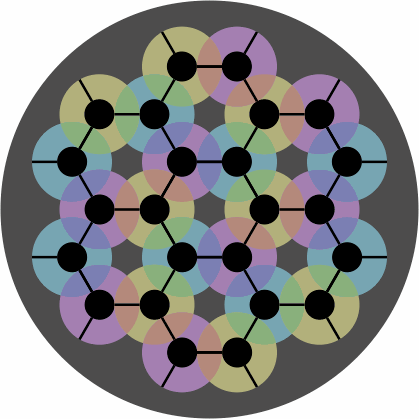
Figure 7 depicts disks in two or three colors, with intermediate hues for their overlap:

figure 7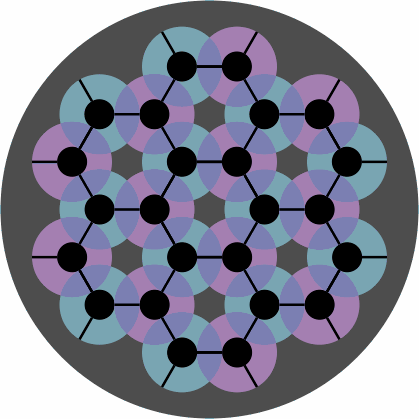

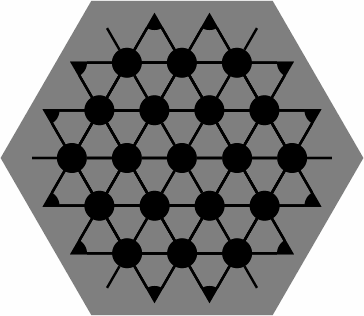
Players might devise special rules that depend on the colors. Alternatively, the disks can be omitted entirely, yielding a diagram that happens to resemble one layer of graphite:

figure 8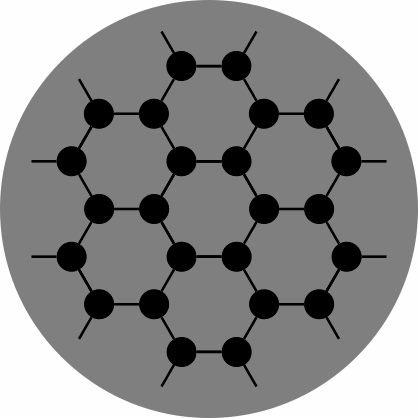

To record the moves of a game, it is convenient that locations have labels. Figure 9 is one way to do it:

figure 9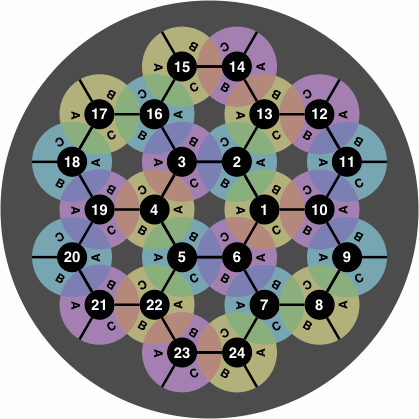

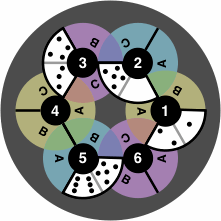
In the following example of how to interpret the labels, tile 1-2 is placed at 1C, 0-5 at 2B, 3-4 at 3A, and 5-6 at 5C:

figure 10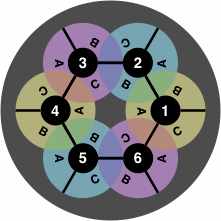

Not all locations can be used simultaneously. For instance, as soon as a tile is tile is placed at 2B, locations 1A and 3C become unavailable. This labeling scheme readily extends to larger boards, for example figure 11:

figure 11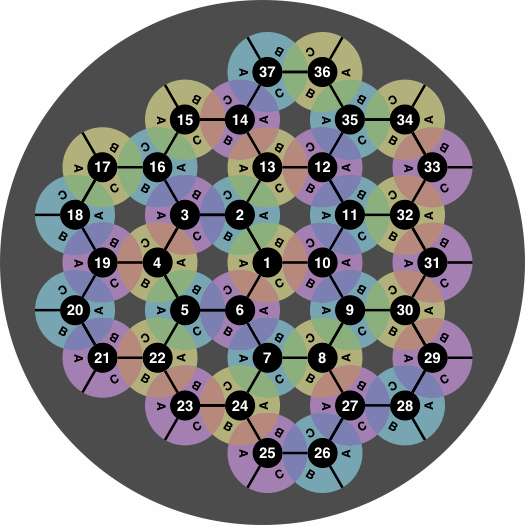

An option is to highlight the spiral pattern of the numbers:

figure 12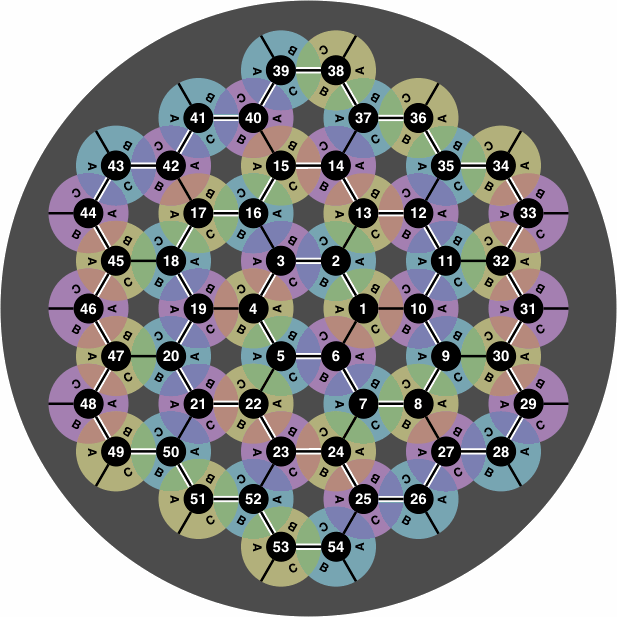

From time to time a student will want to re-enact a game from its transcript, but the student's board may be of a size different from that used for the transcribed game. If manufacturers standardize all boards to be approximately round, with spiral numbering that begins in the center, the student will have the best chance to interpret the transcript with the board he has. Figures 9 through 12 observe this standard.

On the other hand, a non-round board (figure 13) might become necessary if play is confined to a cramped space such as a train or bus. Not obvious is what the best numbering scheme would be.

figure 13

In a variant not manufactured, the two halves of the tile curve opposite directions. To help tell the difference between the two varieties, the tiles that skew left are tinted in yellow, and those that skew right are magenta.

figure 14

Because a large number of such skew tiles are possible, a more manageable set might omit the sixes and fives.

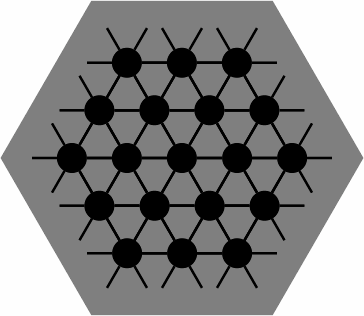
Figure 15 contains three alignment diagrams for skew tiles differing only in closure of the edge; players choose whichever they prefer. They resemble figure 8 but have additional black dots, some of them fractional. The colored disks of figure 4 are left out because there would be too many of them, providing more confusion than guidance.

figure 15
	closed edge	mixed edge	open edge

Figure 16 shows how the edge configuration affects the way that tiles can be played near the edge of the board. As always, each concave curve hugs a black dot, and the ends of a tile fall on black lines. All tiles shown are legal; but with less edge closure, fewer placements are permitted.

figure 16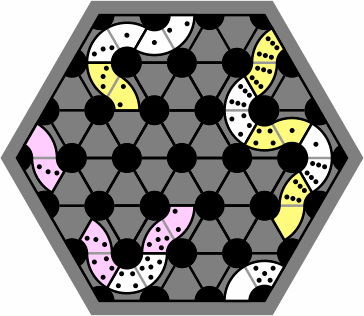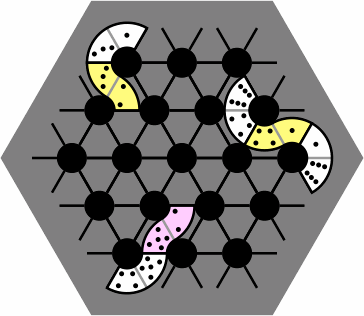

Figure 17 is a sample layout with one long chain of both skew and non-skew tiles, as might appear in a game:

figure 17

At the beginning of most domino games, all the tiles are placed face down and scrambled, and players choose their tiles at random. Because the non-skew, left-skew, and right-skew tiles are distinguishable even when face down, game rules might specify that each player take a certain number of each.

A tile with only one number, roughly triangular in shape, also fits the skew alignment diagram. It has three concave curves, each of which must abut a fractional or whole black dot. Despite having only one number, this tile takes three neighbors and thus permits branching of the layout. It is tinted cyan in the drawings for ease of identification.

figure 18

The degree of edge closure affects placement of the one-number pieces in much the same way as other tiles. Figure 19 corresponds to figure 16:

figure 19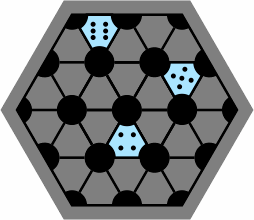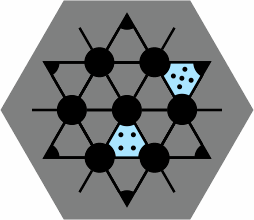
	closed edge	mixed edge	open edge

Figure 20 is an example of how to use them:

figure 20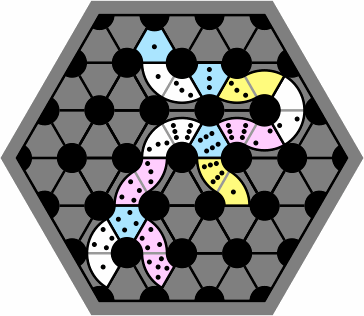

Figure 21 shows a labeling scheme for recording a game. Although it differs from figure 9, it is still a rough spiral starting at the center of the board.

figure 21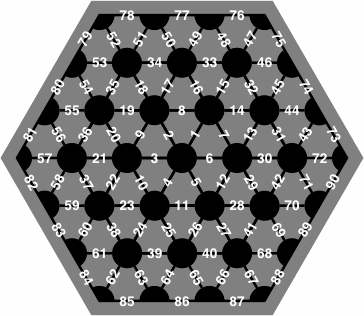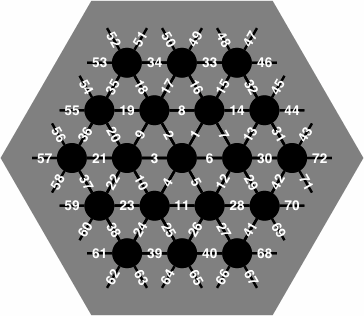
	closed edge	open edge (same numbering for mixed edge)

On the actual board the numbers would likely be printed smaller than suggested by this image, but limitations of computer screen resolution required the numbers to be drawn artificially large for this picture.

The following is a suggested notation for recording the placement of a tile:

• For tiles with two numbers:
  1. Write the numbers of the two lines at the ends of the tile, smaller number first.
  2. Write the pip count abutting the smaller-numbered line, followed by the pip count abutting the larger-numbered line.
• For tiles with one number:
  1. Write the numbers of the two smallest-numbered lines surrounding the tile, smaller number first.
  2. Write the pip count.
• In all cases, separate numbers with hyphens.

Figure 22 contains some examples:

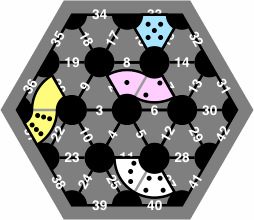
figure 22
	tile left-skew right-skew non-skew one-number notation 20-37-0-6 2-7-1-2 11-27-3-4 15-16-5

Notation 37-20-6-0, which puts the larger line number first, is nonstandard but unambiguous. In contrast, 20-37-6-0 is wrong because in this example the 6 pip does not touch the 20 line.

Players who regard the edge of the board as a needless constraint may obtain a closed-edge diagram and wrap around. In figure 23, the 1-2 at the top is adjacent to the 2-3 at the bottom, both at the X3 marking. Similarly, the 6-0 and 0-4 abut via Z2; likewise for 5-3 and the single 3 via Y2. Hence this layout is one long chain.

figure 23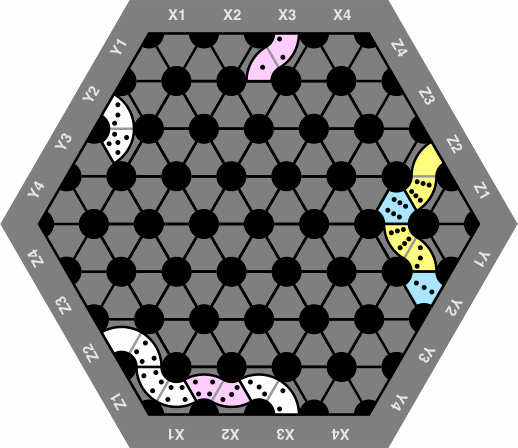

Note that when numbers are added to the wrap-around board, some are repeated:

figure 24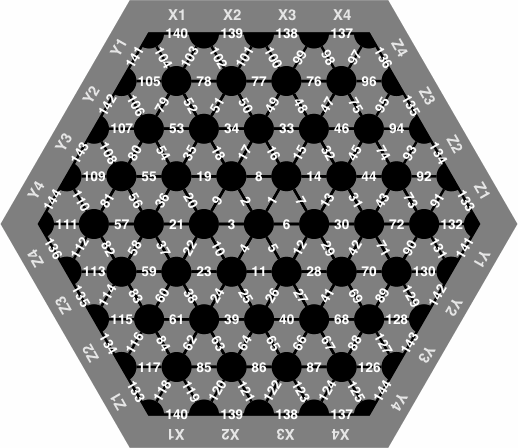

The figures were prepared with Adobe PostScript, the acme of programming languages for graphics.