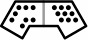
The design of Bendominoes is based upon circular arcs. However, there is a certain octagon which can not only substitute for the arc-based tiles in ordinary play, but which offer additional possibilities of matching. Some examples of polybens (polygonal bendominoes), along with their numerical designations, appear in figure 25:

figure 25
	0-1	2-3	4-5
	6-7	8-9	10-11
	12-13	13-12	6-6

Note that 12-13 is distinct from its mirror image 13-12; for best results a set should never have one of a mirror-image pair without the other. A tile like 6-6 is naturally called a double. The tiles conveniently hold as many as thirteen pips, but a useful set of 36 tiles can be made by going no higher than five, as in figure 26:

figure 26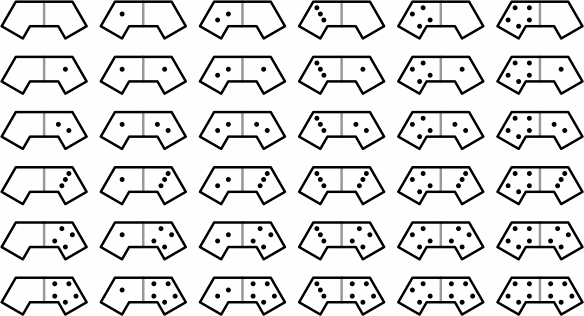

Proportions of the tile, specified in figure 27, are critical, although the entire piece can be made larger or smaller as manufacturers opt. A likely size would have one unit equalling twelve millimeters.

figure 27		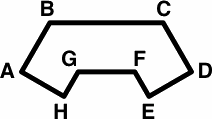length:	1 unit	EF, GH
			√3 ≈ 1.732 units	AH, DE
			2 units	AB, CD, FG
			4 units	BC
		angle:	90 degrees	A, D, E, H
			120 degrees	B, C, F, G

The sides have names:

• shoulder: AB and CD
• back: BC
• belly: FG
• end: AH and DE
• hook: EF and GH

The belly is the same length as a shoulder, or half of the back; the tile was designed this way in order to provide plenty of matching opportunities.

As with curved tiles, three pieces form a loop. Figure 28 corresponds to figure 3 on the curved page:

figure 28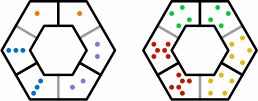

Figure 29, equivalent to figure 5 on the curved page, shows end-to-end matching of polybens. The suggested alignment diagram for polybens is simply a triangular grid of dots, which is noticeably simpler than the diagram for the curved version (figure 7 or figure 15). The number of dots in the grid and its overall shape accord to the preference of the players.

figure 29

When a tile is correctly placed, each of its eight corners (lettered A through H in figure 27) will fall precisely on a dot, as will the ends of the dividing bar in the middle of the tile. The magnification of figure 30 shows this more clearly:

figure 30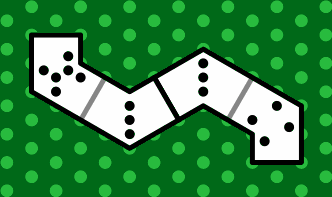

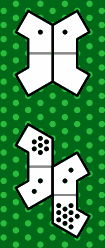
The reason for the polygonal design is to allow the tiles to abut in more ways than in the original circular scheme. Players when negotiating the rules before starting a game will probably choose to allow some, but not all, of the configurations displayed in figure 31:

• 31a: end-to-end matchings, as in figure 29.
• 31b: back-to-back matchings, with 0-1 and 1-0 fullback-to-fullback, and with 11-2 and 7-2 halfback-to-halfback.
• 31c: shoulder-to-shoulder matchings.
• 31d: shoulder-to-halfback matchings.
• 31e: a shoulder abutting the belly of a double (10-6 and 6-6), two tiles (7-4 and 7-13) matched at the hooks, and two tiles (11-8 and 8-5) adjoining hook to half shoulder.

figure 31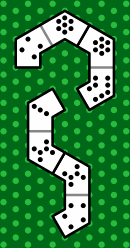
	31a	31b	31c	31d	31e

Notes:

• The fullback-to-fullback arrangement motivates the recommendation above that whatever tiles are included in a set, their mirror images ought also be included.
• As a result of the corners-on-dots rule, an end cannot abut anything except another end.
• Conservative players will likely allow only the matches of 31a and 31b. Liberals might add some of the others. An alternate approach is to use only the back and shoulder abutments of 31b, 31c and 31d, omitting the original end-to-end arrangement of bendominoes.
• As more varieties of adjacency are allowed, the layout becomes less catenative and more tessellative in nature. When this happens, players will want to develop rules and a scoring schedule that generate a game more sophisticated than a mere race to empty their hands of tiles.

Figure 32 shows how three or four tiles might meet at their ends, backs and shoulders:

figure 32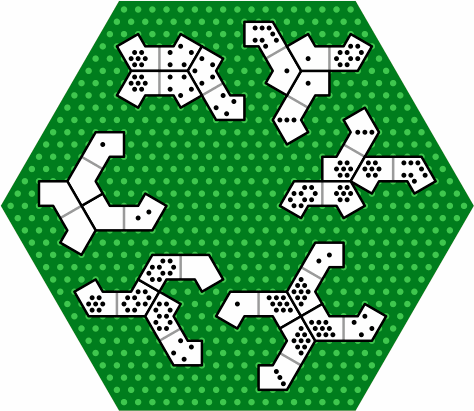

Figure 33 is an example of a complicated layout:

figure 33

A suggested rule is to permit corner-to-corner adjacencies when they arise incidentally from side-to-side adjacencies, if the numbers match. In figure 33, these are 5-4 next to 4-4 in the lower right, and 1-6 next to 6-2 at the left.

Skew tiles naturally ensue. Figure 34 is the octagonal version of figure 14:

figure 34

Figure 35 is equivalent to figure 17. The grid of dots is especially helpful in this layout; without it players might worry about accurate tile placement, and wonder whether the 5-6 and 4-0 skew-right tiles near the center of the picture ought in fact to touch.

figure 35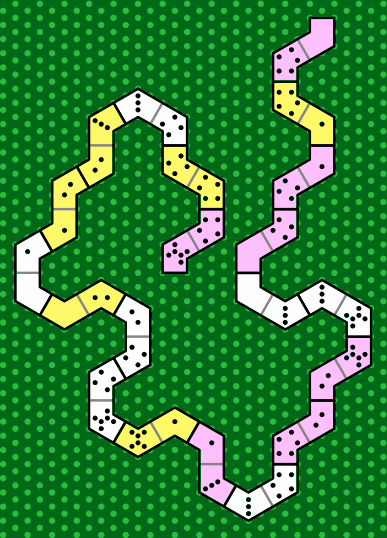

Figure 36, corresponding to figure 18 on the curved page, introduces single-number polygonal (more specifically, enneagonal) tiles.

• With the circular design of original Bendominoes, single-number tiles were the only obvious method of establishing branches, as shown in figure 20 on the curved page. Without such branching, tile placement is restricted to one chain, giving players relatively few options in play.
• With polygonal tiles on the other hand, the multiple categories of adjacency (figure 31) permit plenty of branching for players who want it; hence these single-number tiles wane in importance.

figure 36

The sides of the single-number tiles come in only two lengths, the shorter being hooks and the longer being ends. In terms of the dimensions given in figure 27, the hooks are 1 unit, the ends √3 units, and the angles 90 or 120 degrees.

Besides containing tiles equivalent to those of figure 20, figure 37 includes many others to illustrate possible tile adjacencies. Players can decide which categories of adjacency they want to recognize.

figure 37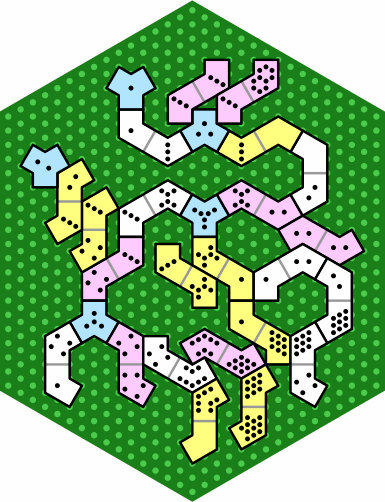

Yet another shape of tile results from putting the two halves of a tile together along a shoulder, or equivalently half a back:

figure 38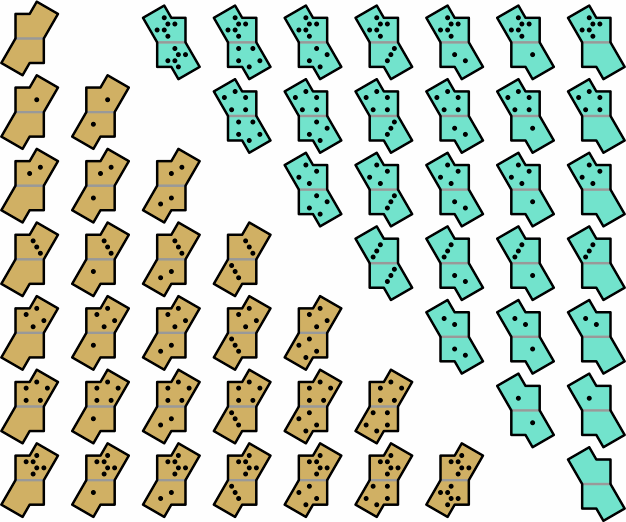

These decagonal pieces can fully participate in tessellations with the octagonal tiles of figures 26 and 34, and the enneagonal of figure 36. They have no obvious counterpart among the curved tiles.

The figures were prepared with Adobe PostScript, the acme of programming languages for graphics.