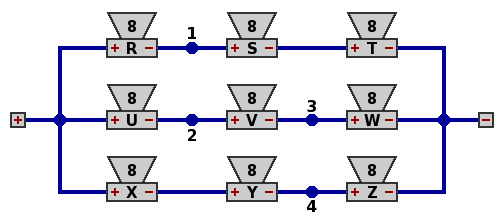
Circuit 1, below, has nine identical speakers arranged into three parallel branches, each containing three speakers in series. Assume each speaker has an impedance of 8 ohms, and is supplied with enough current to be dissipating 10 watts. Easily calculated are that the overall impedance of the network is 8 ohms, and the overall power dissipation is 90 watts.

Circuit 1.

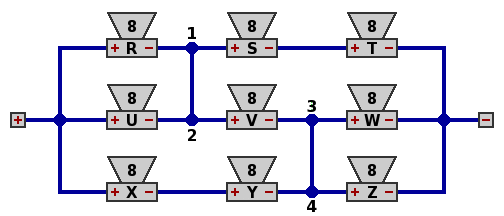
From symmetry, node 1 must be at the same voltage as node 2, so if they are connected as in circuit 2, below, there will be no current in the linking wire. Similarly connect nodes 3 and 4 with a wire. The electrical properties of the network, and all the component speakers, are the same.

Circuit 2.

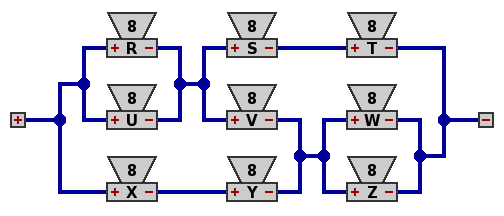
Now rearrange the wires to emphasize certain connections, as in circuit 3.

Circuit 3.

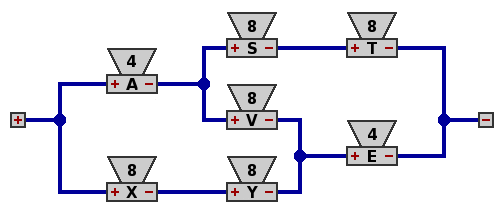
To obtain circuit 4, replace 8Ω speakers R and U, which are in parallel, with 4Ω speaker A, which will necessarily dissipate 20 watts. Similarly, replace W and Z with 4Ω speaker E.

Circuit 4.

To obtain circuit 5, replace speakers S and T, which are in series, with 16Ω speaker D, which will also dissipate 20 watts. Similarly, replace X and Y with 16Ω speaker B.

Circuit 5.

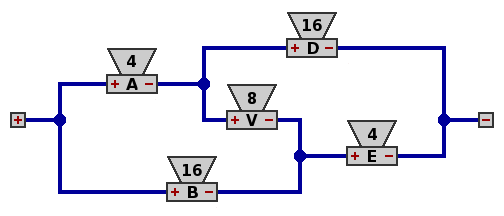
Rename speaker V as C, and rearrange the wires to reveal the familiar drawing of the canonical network as in circuit 6.

Circuit 6.
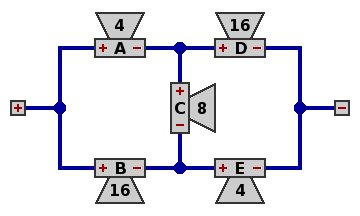