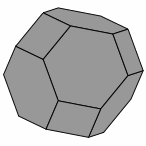
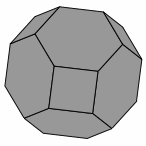
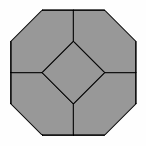
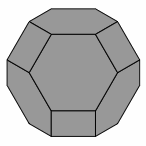
— Figure one —
The Tantrix ROCK is a three-dimensional puzzle where the player tries to assemble eight hexagonal tiles and six square tiles into a truncated octahedron. Here are several views of that shape:




— Figure one —
The challenge of the puzzle is that each tile has markings which must match where one tile adjoins another. More specifically, the manufacturer paints paths, straight or curved, on each tile with each path connecting the middle of one edge with another. Consequently, a hexagonal tile has three paths and a square tile has two; paths sometimes cross each other. By convention, all paths on a tile are different colors, typically yellow, red and blue. A green stripe is also found on some non-ROCK versions of Tantrix, which usually involve tessallating hexagons on a plane.
Rather than colors, this report uses single, double or triple stripes in deference to people who have difficulty distinguishing colors; there is also an advantage should the images be printed or viewed on a monochrome device. The logic of the puzzle is the same.
An extended discussion of Tantrix is found at Jaap.
Tiles can exhibit any of the configurations in table one; under each is written a label for reference.
| Table one | |||||||
|---|---|---|---|---|---|---|---|
 6:0 |  6:2 |  6:5 | 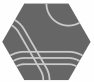 6:8 |  6:B |  6:E |  4:0 |  4:3 |
 6:1 |  6:3 |  6:6 |  6:9 |  6:C |  6:F |  4:1 |  4:4 |
 6:4 |  6:7 |  6:A |  6:D |  4:2 |  4:5 | ||
The factory supplies only eight hexagonal tiles with the ROCK, and they have yellow, blue or red stripes. Under the following equivalences…
Our analysis will assume that all sixteen hexagons are available, although only eight can be used at a time; then 476 solutions will be generated.
The factory usually omits tiles 6:E and 6:F, containing only straight lines, from those Tantrix sets intended for plane tessellation. This is because those tiles have only three distinct rotations rather than six, and this lack is felt to give players insufficient flexibility. If Tantrix ROCK is similarly constrained, only 208 solutions will be possible.
All six square tiles are required in every solution.
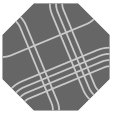
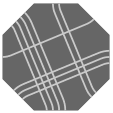
Here are several views of one solution:
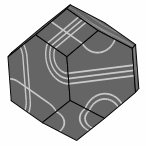

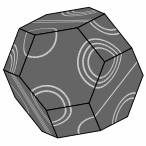
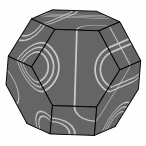

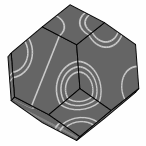
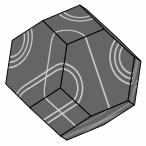
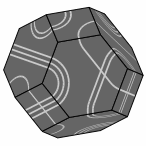
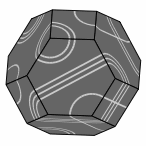
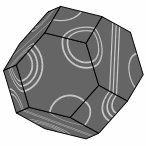
— Figure two —
Although such pictorial images are helpful, they cannot show all tiles at once. An alternative is to arrange tiles as though the truncated octahedron is cut apart along certain edges, forming a net:
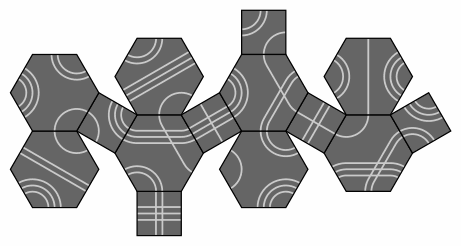
— Figure three —
Such a cut-apart drawing requires about 11 kilobytes, which if produced for each of the 476 solutions would require exorbitant amounts of memory. Our presentation of the solutions instead uses a separate image for each tile, at some loss of clarity:
 | |||||||
  | 
|   | 
|   | 
|   | 
|
 | |||||||
| — Figure four — | |||||||
Because images are reused from one solution to the next, memory demands and download time are greatly reduced. A lengthy table contains all solutions.
Although not chosen for this report, a more compact representation is possible, as in figure five. Because placement of the squares is trivial once the hexagons are established, the squares could be omitted entirely.
 
|  
|  
|  
| ||||
| — Figure five — | |||||||
Different combinations of hexagons offer different numbers of solutions. In table two, the "6:" has been omitted for clarity.
| Table two | |||
|---|---|---|---|
| Each has 12 solutions: • 0 1 2 3 4 5 8 E • 0 1 2 3 4 5 8 F • 0 1 2 3 4 6 9 E • 0 1 2 3 4 6 9 F • 0 1 2 3 4 7 A E • 0 1 2 3 4 7 A F | Each has 5 solutions: • 0 2 3 5 6 9 B C • 0 2 3 5 7 A B C • 0 2 4 5 7 8 B D • 0 2 4 6 7 9 B D • 0 3 4 5 6 8 C D • 0 3 4 6 7 A C D • 1 2 3 6 8 9 B C • 1 2 3 7 8 A B C • 1 2 4 5 8 A B D • 1 2 4 6 9 A B D • 1 3 4 5 8 9 C D • 1 3 4 7 9 A C D | Each has 4 solutions: • 0 1 2 3 4 5 6 7 • 0 1 2 3 4 8 9 A • 0 1 5 6 7 B C D • 0 1 8 9 A B C D • 0 2 3 6 7 B C F • 0 2 4 5 6 B D F • 0 3 4 5 7 C D F • 1 2 3 9 A B C E • 1 2 4 8 9 B D E • 1 3 4 8 A C D E | Each has 3 solutions: • 0 2 5 6 7 8 D F • 0 2 5 6 7 A C F • 0 3 5 6 7 8 D F • 0 3 5 6 7 9 B F • 0 4 5 6 7 9 B F • 0 4 5 6 7 A C F • 1 2 5 8 9 A D E • 1 2 7 8 9 A C E • 1 3 5 8 9 A D E • 1 3 6 8 9 A B E • 1 4 6 8 9 A B E • 1 4 7 8 9 A C E |
Meanwhile, 68 combinations have two solutions, and 132 have one. This leaves 12630 combinations of hexagonal tiles that give no solution at all.
If all 16 hexagonal tiles are available, then once a solution is obtained, certain operations can yield more solutions. Details of twelve operations are in table three, but a few of them are enough to generate the others:
Table three shows which tiles are replaced by which others under each operation. Consider for instance exchanging singles and triples (rc3) within an old solution to obtain a new solution. In the rc3 column of the upper part of the table, the expression 6:A >> 6:5 means that if the tile 6:A was in the old solution, 6:5 will be installed in the new solution, in whatever location 6:A had been. Tile 6:A might ultimately be used elsewhere in the new solution, or be discarded. By the same token, 6:5 may or may not have appeared in the old solution.
The difference between the upper part (rc) and the lower part (rt) is that operations in the lower also involve reflecting the solution. To denote this difference, column headers use single-shaft arrows in the upper part, and double-shaft in the lower. In the operation names, r stands for rearrangement, c for cis, and t for trans.
In a fuller example, the hexagonal tiles of solution 283 — 6:0, 6:2, 6:5, 6:6, 6:7, 6:9, 6:A and 6:D — would under operation rt4 become the hexagon tiles of solution 459 — 6:1, 6:4, 6:A, 6:8, 6:9, 6:5, 6:6 and 6:C respectively.
Although all square tiles are used in every solution, they are included in the tables to show how they move around. For example, tiles 4:0 and 4:1 trade places in rt3.
Operations can be performed one after the other, but the sequence often makes a difference. For example, first exchanging single and double stripes (rc1), and then exchanging double and triple stripes (rc5), is equivalent to changing singles to triples, doubles to singles, and triples to doubles (rc4). On the other hand, rc5 followed by rc1 gives rc2 instead.
| Table three | ||||||
|---|---|---|---|---|---|---|
| without reflection | rc0 single → single double → double triple → triple | rc1 single → double double → single triple → triple | rc2 single → double double → triple triple → single | rc3 single → triple double → double triple → single | rc4 single → triple double → single triple → double | rc5 single → single double → triple triple → double |
| 6:0 >> 6:0 6:1 >> 6:1 6:2 >> 6:2 6:3 >> 6:3 6:4 >> 6:4 6:5 >> 6:5 6:6 >> 6:6 6:7 >> 6:7 6:8 >> 6:8 6:9 >> 6:9 6:A >> 6:A 6:B >> 6:B 6:C >> 6:C 6:D >> 6:D 6:E >> 6:E 6:F >> 6:F | 6:0 >> 6:1 6:1 >> 6:0 6:2 >> 6:4 6:3 >> 6:3 6:4 >> 6:2 6:5 >> 6:9 6:6 >> 6:8 6:7 >> 6:A 6:8 >> 6:6 6:9 >> 6:5 6:A >> 6:7 6:B >> 6:D 6:C >> 6:C 6:D >> 6:B 6:E >> 6:F 6:F >> 6:E | 6:0 >> 6:0 6:1 >> 6:1 6:2 >> 6:3 6:3 >> 6:4 6:4 >> 6:2 6:5 >> 6:6 6:6 >> 6:7 6:7 >> 6:5 6:8 >> 6:9 6:9 >> 6:A 6:A >> 6:8 6:B >> 6:C 6:C >> 6:D 6:D >> 6:B 6:E >> 6:E 6:F >> 6:F | 6:0 >> 6:1 6:1 >> 6:0 6:2 >> 6:2 6:3 >> 6:4 6:4 >> 6:3 6:5 >> 6:A 6:6 >> 6:9 6:7 >> 6:8 6:8 >> 6:7 6:9 >> 6:6 6:A >> 6:5 6:B >> 6:B 6:C >> 6:D 6:D >> 6:C 6:E >> 6:F 6:F >> 6:E | 6:0 >> 6:0 6:1 >> 6:1 6:2 >> 6:4 6:3 >> 6:2 6:4 >> 6:3 6:5 >> 6:7 6:6 >> 6:5 6:7 >> 6:6 6:8 >> 6:A 6:9 >> 6:8 6:A >> 6:9 6:B >> 6:D 6:C >> 6:B 6:D >> 6:C 6:E >> 6:E 6:F >> 6:F | 6:0 >> 6:1 6:1 >> 6:0 6:2 >> 6:3 6:3 >> 6:2 6:4 >> 6:4 6:5 >> 6:8 6:6 >> 6:A 6:7 >> 6:9 6:8 >> 6:5 6:9 >> 6:7 6:A >> 6:6 6:B >> 6:C 6:C >> 6:B 6:D >> 6:D 6:E >> 6:F 6:F >> 6:E | |
| 4:0 >> 4:0 4:1 >> 4:1 4:2 >> 4:2 4:3 >> 4:3 4:4 >> 4:4 4:5 >> 4:5 | 4:0 >> 4:0 4:1 >> 4:2 4:2 >> 4:1 4:3 >> 4:3 4:4 >> 4:5 4:5 >> 4:4 | 4:0 >> 4:1 4:1 >> 4:2 4:2 >> 4:0 4:3 >> 4:4 4:4 >> 4:5 4:5 >> 4:3 | 4:0 >> 4:1 4:1 >> 4:0 4:2 >> 4:2 4:3 >> 4:4 4:4 >> 4:3 4:5 >> 4:5 | 4:0 >> 4:2 4:1 >> 4:0 4:2 >> 4:1 4:3 >> 4:5 4:4 >> 4:3 4:5 >> 4:4 | 4:0 >> 4:2 4:1 >> 4:1 4:2 >> 4:0 4:3 >> 4:5 4:4 >> 4:4 4:5 >> 4:3 | |
| with reflection | rt0 single ⇒ single double ⇒ double triple ⇒ triple | rt1 single ⇒ double double ⇒ single triple ⇒ triple | rt2 single ⇒ double double ⇒ triple triple ⇒ single | rt3 single ⇒ triple double ⇒ double triple ⇒ single | rt4 single ⇒ triple double ⇒ single triple ⇒ double | rt5 single ⇒ single double ⇒ triple triple ⇒ double |
| 6:0 >> 6:1 6:1 >> 6:0 6:2 >> 6:2 6:3 >> 6:3 6:4 >> 6:4 6:5 >> 6:8 6:6 >> 6:9 6:7 >> 6:A 6:8 >> 6:5 6:9 >> 6:6 6:A >> 6:7 6:B >> 6:B 6:C >> 6:C 6:D >> 6:D 6:E >> 6:F 6:F >> 6:E | 6:0 >> 6:0 6:1 >> 6:1 6:2 >> 6:4 6:3 >> 6:3 6:4 >> 6:2 6:5 >> 6:6 6:6 >> 6:5 6:7 >> 6:7 6:8 >> 6:9 6:9 >> 6:8 6:A >> 6:A 6:B >> 6:D 6:C >> 6:C 6:D >> 6:B 6:E >> 6:E 6:F >> 6:F | 6:0 >> 6:1 6:1 >> 6:0 6:2 >> 6:3 6:3 >> 6:4 6:4 >> 6:2 6:5 >> 6:9 6:6 >> 6:A 6:7 >> 6:8 6:8 >> 6:6 6:6 >> 6:7 6:A >> 6:5 6:B >> 6:C 6:C >> 6:D 6:D >> 6:B 6:E >> 6:F 6:F >> 6:E | 6:0 >> 6:0 6:1 >> 6:1 6:2 >> 6:2 6:3 >> 6:4 6:4 >> 6:3 6:5 >> 6:7 6:6 >> 6:6 6:7 >> 6:5 6:8 >> 6:A 6:9 >> 6:9 6:A >> 6:8 6:B >> 6:B 6:C >> 6:D 6:D >> 6:C 6:E >> 6:E 6:F >> 6:F | 6:0 >> 6:1 6:1 >> 6:0 6:2 >> 6:4 6:3 >> 6:2 6:4 >> 6:3 6:5 >> 6:A 6:6 >> 6:8 6:7 >> 6:9 6:8 >> 6:7 6:9 >> 6:5 6:A >> 6:6 6:B >> 6:D 6:C >> 6:B 6:D >> 6:C 6:E >> 6:F 6:F >> 6:E | 6:0 >> 6:0 6:1 >> 6:1 6:2 >> 6:3 6:3 >> 6:2 6:4 >> 6:4 6:5 >> 6:5 6:6 >> 6:7 6:7 >> 6:6 6:8 >> 6:8 6:9 >> 6:A 6:A >> 6:9 6:B >> 6:C 6:C >> 6:B 6:D >> 6:D 6:E >> 6:E 6:F >> 6:F | |
| 4:0 >> 4:0 4:1 >> 4:1 4:2 >> 4:2 4:3 >> 4:3 4:4 >> 4:4 4:5 >> 4:5 | 4:0 >> 4:0 4:1 >> 4:2 4:2 >> 4:1 4:3 >> 4:3 4:4 >> 4:5 4:5 >> 4:4 | 4:0 >> 4:1 4:1 >> 4:2 4:2 >> 4:0 4:3 >> 4:4 4:4 >> 4:5 4:5 >> 4:3 | 4:0 >> 4:1 4:1 >> 4:0 4:2 >> 4:2 4:3 >> 4:4 4:4 >> 4:3 4:5 >> 4:5 | 4:0 >> 4:2 4:1 >> 4:0 4:2 >> 4:1 4:3 >> 4:5 4:4 >> 4:3 4:5 >> 4:4 | 4:0 >> 4:2 4:1 >> 4:1 4:2 >> 4:0 4:3 >> 4:5 4:4 >> 4:4 4:5 >> 4:3 | |
These twelve operations form a symmetry group. Operation rc0, which changes nothing, is the identity element.
Table four shows all the possibilities when one operation comes after another. For example, if rc3 is followed by rt2, the effect is the same as if rt5 alone had been performed.
| Table four | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
second operation
| rc0 | rc1 | rc2
| rc3 | rc4 | rc5
| rt0 | rt1 | rt2
| rt3 | rt4 | rt5
| first | operation rc0
| rc0 | rc1
| rc2 | rc3
| rc4 | rc5
| rt0 | rt1
| rt2 | rt3
| rt4 | rt5
| rc1
| rc1 | rc0
| rc3 | rc2
| rc5 | rc4
| rt1 | rt0
| rt3 | rt2
| rt5 | rt4
| rc2
| rc2 | rc5
| rc4 | rc1
| rc0 | rc3
| rt2 | rt5
| rt4 | rt1
| rt0 | rt3
| rc3
| rc3 | rc4
| rc5 | rc0
| rc1 | rc2
| rt3 | rt4
| rt5 | rt0
| rt1 | rt2
| rc4
| rc4 | rc3
| rc0 | rc5
| rc2 | rc1
| rt4 | rt3
| rt0 | rt5
| rt2 | rt1
| rc5
| rc5 | rc2
| rc1 | rc4
| rc3 | rc0
| rt5 | rt2
| rt1 | rt4
| rt3 | rt0
| rt0
| rt0 | rt1
| rt2 | rt3
| rt4 | rt5
| rc0 | rc1
| rc2 | rc3
| rc4 | rc5
| rt1
| rt1 | rt0
| rt3 | rt2
| rt5 | rt4
| rc1 | rc0
| rc3 | rc2
| rc5 | rc4
| rt2
| rt2 | rt5
| rt4 | rt1
| rt0 | rt3
| rc2 | rc5
| rc4 | rc1
| rc0 | rc3
| rt3
| rt3 | rt4
| rt5 | rt0
| rt1 | rt2
| rc3 | rc4
| rc5 | rc0
| rc1 | rc2
| rt4
| rt4 | rt3
| rt0 | rt5
| rt2 | rt1
| rc4 | rc3
| rc0 | rc5
| rc2 | rc1
| rt5
| rt5 | rt2
| rt1 | rt4
| rt3 | rt0
| rc5 | rc2
| rc1 | rc4
| rc3 | rc0
| | |||||||||||||
Based on what can be exchanged with what else in the operations, one can partition the tiles into subsets:
| Table five | |
|---|---|
| S0 | 4:0, 4:1, 4:2 |
| S1 | 4:3, 4:4, 4:5 |
| H0 | 6:0, 6:1 |
| H1 | 6:2, 6:3, 6:4 |
| H2 | 6:5, 6:6, 6:7, 6:8, 6:9, 6:A |
| H3 | 6:B, 6:C, 6:D |
| H4 | 6:E, 6:F |
This will be helpful in the following section.
Each row of table six below shows a set of solutions that is closed under the twelve operations. Most sets have 12 members, but some have fewer.
The members of each set are presented in a particular sequence of operations of its first member. Note that the choice of first member was arbitary; any other member would have been just as good.
Each number refers to the solution's position in the lengthy table.
Taking the first row as an example, 6 = rc0(6), 63 = rc1(6), 35 = rc2(6), 33 = rc3(6) et cetera. All the tiles for these solutions come from partitions H0 (6:0 and 6:1), H1 (6:2 through 6:4) and H2 (6:5 through 6:A). Tiles 6:B through 6:F are not needed.
| Table six | |
|---|---|
| Solutions | Partitions |
| 6, 63, 35, 33, 8, 38; 64, 5, 34, 36, 37, 7 | H0, H1, H2 |
| 1, 90; 91, 3 | |
| 2, 92; 89, 4 | |
| 215, 219; 218, 216 | H0, H2, H3 |
| 213, 217 | |
| 214, 220 | |
| 93, 164, 161, 126, 118, 102; 99, 153, 166, 120, 124, 97 | H0, H1, H2, H3 |
| 239, 428, 299, 393, 251, 372; 366, 298, 435, 252, 383, 240 | |
| 226, 423, 309, 394, 263, 367; 365, 297, 438, 269, 388, 233 | |
| 135, 205, 186, 151, 198, 182; 140, 195, 189, 146, 209, 179 | |
| 279, 459, 323, 412, 332, 447; 407, 331, 452, 283, 460, 319 | |
| 228, 424, 312, 397, 260, 370; 363, 293, 439, 273, 385, 234 | |
| 138, 211, 174, 142, 201, 188; 150, 204, 181, 137, 207, 175 | |
| 136, 208, 176, 149, 203, 180; 141, 202, 187, 139, 212, 173 | |
| 225, 425, 311, 395, 261, 371; 364, 296, 437, 270, 387, 236 | |
| 229, 427, 310, 396, 262, 368; 361, 294, 436, 272, 386, 235 | |
| 245, 421, 316, 391, 264, 358; 354, 304, 432, 274, 381, 248 | |
| 237, 422, 315, 392, 277, 357; 353, 314, 431, 278, 382, 238 | |
| 227, 426, 313, 398, 259, 369; 362, 295, 440, 271, 384, 232 | |
| 340, 418, 287, 458, 327, 469; 470, 288, 417, 328, 457, 339 | |
| 94, 163, 160, 125, 117, 101; 100, 154, 165, 121, 123, 96 | |
| 29, 41, 55, 70, 86, 15; 13, 56, 40, 83, 75, 26 | H0, H1, H2, H4 |
| 57, 9, 84, 46, 25, 76; 44, 30, 74, 54, 19, 88 | |
| 43, 23, 71, 58, 12, 77; 52, 18, 82, 50, 32, 73 | |
| 11, 60, 48, 81, 67, 22; 31, 47, 53, 69, 78, 16 | |
| 224, 419, 308, 389, 258, 355; 351, 291, 429, 268, 380, 230 | |
| 45, 28, 68, 59, 20, 79; 61, 10, 85, 42, 27, 66 | |
| 51, 17, 87, 39, 24, 72; 49, 21, 65, 62, 14, 80 | |
| 223, 420, 307, 390, 257, 356; 352, 292, 430, 267, 379, 231 | |
| 134, 193, 185, 144, 197, 177; 133, 194, 184, 145, 196, 178 | |
| 221, 350; 349, 222 | H0, H1, H3, H4 |
| 344, 473, 346, 476, 347, 471; 472, 345, 474, 348, 475, 343 | H0, H2, H3, H4 |
| 244, 443, 300, 403, 253, 374; 373, 301, 442, 255, 404, 241 | H0, H1, H2, H3, H4 |
| 243, 441, 302, 401, 254, 375; 376, 303, 444, 256, 402, 242 | |
| 286, 465, 322, 410, 333, 453; 413, 336, 450, 281, 463, 324 | |
| 116, 127, 106, 109, 158, 169; 128, 115, 110, 105, 168, 159 | |
| 276, 405, 250, 377, 306, 446; 406, 266, 378, 247, 445, 318 | |
| 148, 210, 191, 143, 199, 190; 152, 200, 183, 147, 206, 192 | |
| 131, 122, 107, 98, 172, 155; 119, 132, 95, 108, 162, 167 | |
| 249, 434, 305, 399, 275, 359; 360, 317, 433, 265, 400, 246 | |
| 280, 461, 326, 415, 338, 448; 408, 334, 455, 285, 466, 320 | |
| 282, 462, 325, 414, 337, 449; 409, 335, 454, 284, 467, 321 | |
| 156, 111, 113, 170, 103, 129; 171, 104, 130, 157, 112, 114 | |
| 290, 468, 329, 411, 341, 456; 416, 342, 451, 289, 464, 330 | |
Every solution uses at least one member of H0.
A different puzzle can be created by using the fourteen tiles in table seven. It retains five tiles from table one, but introduces nine other tiles with four-stripe arcs.
| Table seven | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 4:0 |  4:1 |  4:2 |  new |  new |  new | ||||||
 6:0 |  6:1 |  new |  new | ||||||||
 new |  new |  new |  new | ||||||||
The rule is the same: form a truncated octahedron, and wherever two tiles adjoin match the number of stripes. Here is one solution:
 | |||||||
  | 
|   | 
|   | 
|   | 
|
 | |||||||
| — Figure six — | |||||||
There are four solutions in total, one obtained from another by applying either or both of these operations:
| Table eight | |
|---|---|
| without reflection: single → single double → double triple → quadruple quadruple → triple | with reflection: single ⇒ single double ⇒ double triple ⇒ triple quadruple ⇒ quadruple |
A property of the truncated octahedron is that, at each vertex, two hexagons and one square meet. What happens if this is changed to one hexagon and two squares? A much simpler puzzle, in the shape of a hexagonal prism, ensues. Here is one solution:
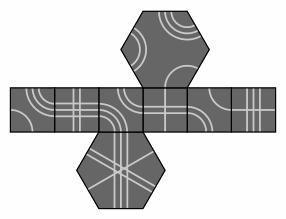
— Figure seven —
All other solutions are related to this one by the rcn and rtn operations.
A further step is to have no hexagons and three squares at each vertex, forming a cube. In this case, however, no solution exists. On the other hand, with three hexagons and no squares at each vertex, the shape becomes a plane tessellation and results in the most popular version of the Tantrix puzzle.
Besides squares and hexagons, a polygon that has an even number of sides is the octagon. Among possible ROCK variant shapes are:
With eight sides, an octagonal tile would have four paths, presumably marked with four colors or four multiplicities of stripes. Recall that table five partitions the squares into two subsets and the hexagons into five; for octagons there would be fully eighteen comparable subsets. In table nine are shown one member of each subset and the subset's name.
| Table nine | ||||||
|---|---|---|---|---|---|---|
| 6 permutations each |  O0 |  O1 | 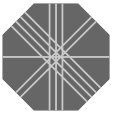 O2 | |||
| 12 permutations each |  O3 | 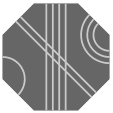 O4 | 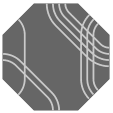 O5 | 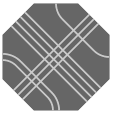 O6 | 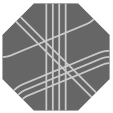 O7 | |
| 24 permutations each |  O8 | 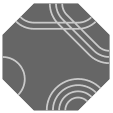 O9 | 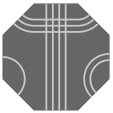 O10 | 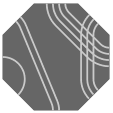 O11 |  O12 | |
 O13 |  O14 |  O15 | 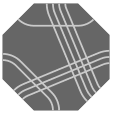 O16 | 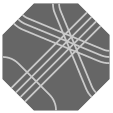 O17 | ||
Because, for most configurations there are 24 permutations of path markings (hence 24 possible tiles), octagonal pieces could easily become too numerous and complicated for enjoyable play. Likely then is that any puzzle using octagonal tiles would include only a judiciously chosen few. Noteworthy is that each of sets O0, O1, and O2 has only six permutations, which is precisely the number of octagonal faces in a truncated cuboctahedron; this fact is perhaps an avenue to an elegant selection of tiles.
By way of example, these are the six members of O1:
| Table ten | ||||||
|---|---|---|---|---|---|---|
| 
| 
| ||||

| 
| 
| ||||
Rhombi are used in another variation.
Miscellaneous.
Images were described in Abobe PostScript; two-dimensional images came from hand-written files, while code for three-dimensional images was generated by a C++ program under XCode. The PostScript code was then converted to pdf using pstopdf. The pdf was then converted to gif with Preview. Most of the html was hand-written, although the lengthy table was generated by the same C++ program that calculated the solutions.
Throughout geometry, there are many octahedra, and many ways to truncate them. However, the term truncated octahedron is almost always taken to mean that all vertices of a regular octahedron have been truncated in such fashion that an equilateral tetradecahedron results. Often overlooked is that the edges of a cube can be truncated to give the same figure.
A candidate solution is any arrangement where 8 hexagonal and 6 square tiles have been physically fitted onto the ROCK. whether or not the stripes match at adjacencies. Fans of big numbers will enjoy learning that there are 7,474,701,359,539,814,400 (7 quintillion or 7 trillion, depending on scale) candidates. However, not all candidate solutions need be examined directly: when two adjacent tiles do not match in an incomplete candidate solution, there is no use trying to complete the candidate. The author used a brute-force search that required about 30 hours of programming time and under 5 minutes of running time on an iMac computer.