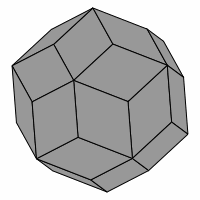
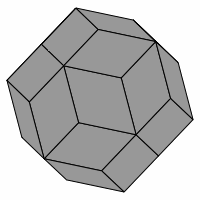
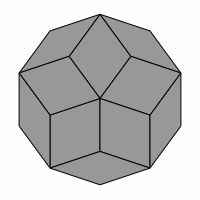
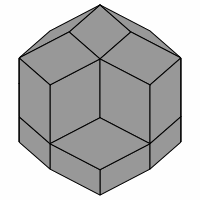
— Figure one —
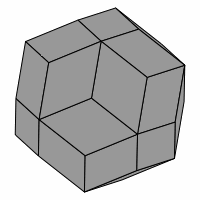
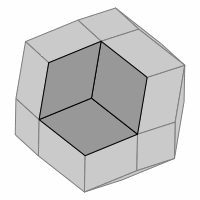
Proposed in this report is a puzzle similar to Tantrix ROCK. Named LAMBDA-ROCK, it is a three-dimensional puzzle in the shape of a rhombic triacontahedron. Here are several views of that shape:




— Figure one —
Care must be used in interpreting these pictures, as some parts of them deceptively resemble an axonometric projection of a cube, as emphasized in figure two. However, no cube is involved.
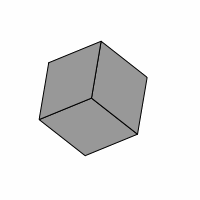
— Figure two —
To solve the puzzle, the player arranges 30 rhombus-shaped tiles on its surface. As with other Tantrix-family puzzles, each tile has markings which must match those on adjacent tiles. On this page, the markings are multiple stripes that connect one edge to another. Other indicators, such as various colors, are possible.
All tiles are rhombi of equal shape and size, although the markings vary. Of any tile, the ratio of the longer diagonal to the shorter is 0.5 × (1 + √5).
The name 30-ROCK with Arabic numerals was considered, but that happens to be the name of a television show. Meanwhile, Roman numerals are of no greater help as XXX-ROCK sounds pornographic. Hence a Greek numeral for thirty was chosen instead, yielding LAMBDA-ROCK or Λ-ROCK.
Table 1 shows how the multiple stripes are drawn. Three single stripes are sometimes coalesced into one triple stripe to make counting easier. There is even a septuple stripe, although it will not be needed in this report. Stripes have a curve at the end so that they will be perpendicular to the edge of the rhombus where they intersect.
| Table 1 | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |

| 
| 
| 
| 
| 
| 
|
| 1 single | 2 singles | 1 triple | 4 singles | 1 double 2 singles | 2 doubles | 1 septuple |
Table 2 shows the sixty tiles considered on this page for solutions of the LAMBDA-ROCK, although only thirty can be used at a time. Each tile has a label of one letter and two digits.
| Table 2 | ||||||
|---|---|---|---|---|---|---|
 | 
|  | 
|  | 
| |
 |  |  | 
|  | 
| |
 | 
|  | 
|  | 
| |
 | 
|  |  |  | 
| |
 | 
|  | 
|  | 
| |
 | 
|  | 
|  | 
| |
 |  |  | 
|  | 
| |
 | 
|  | 
|  | 
| |
 | 
|  |  |  | 
| |
 | 
|  | 
|  | 
| |
We regard segments in the A- and B-series as curved. On the other hand, segments in the C- and D-series are deemed straight, despite the slight twist they exhibit.
Two solutions are pictured as nets below, with dotted lines connecting some of the corners that meet when the figure is folded shut.
Figure three is a solution that requires no more than five stripes on any tile:
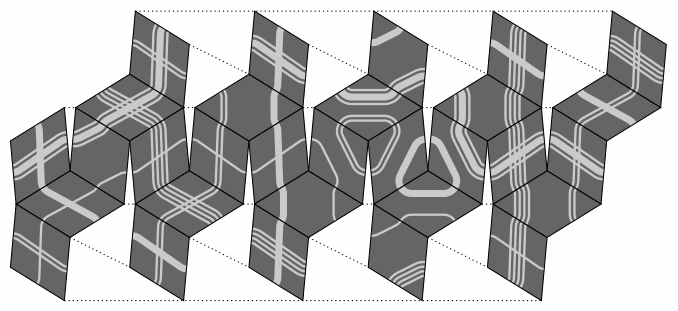
— Figure three —
Figure four, resembling a plaid, uses only pieces from the C and D series:
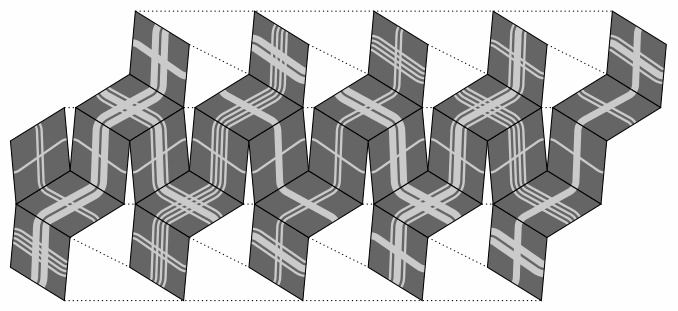
— Figure four —
A path that contains only straight segments will pass through exactly ten tiles, and is analogous to the earth's equator.
There is no solution using only the 15 A-series and 15 B-series tiles pictured above, nor is there one if the two series are extended to include seven-stripe tiles. The existence of a solution that uses eight-stripe tiles is an open question.
Is LAMBDA-ROCK more difficult a puzzle than ROCK? The answer, yet unknown, depends on which of two opposing factors will dominate:
A reasonable challenge with LAMBDA-ROCK is to give the player a list of thirty tiles that can be assembled into a solution, and to let the player seek it.