This report looks at a class of polygons meeting these criteria:

• The polygon does not intersect itself.
• The angle between any two sides is a multiple of 36°.
• All sides are either:
  • One unit long, or
  • φ units long, where φ is the golden ratio, approximately 1.618034.

Such a figure we call a deciphi, from deci- (36° being one-tenth of a circle) and -phi (Greek letter φ denoting the golden ratio). A deciphi can be categorized as:

• proper if the angle between any two adjacent sides is 36°, 72°, 108°, 144°, 216°, 252°, 288° or 324°
• convex if each angle is 36°, 72°, 108° or 144°
• obtuse if each angle is 108° or 144°

The obtuse deciphis form a subset of the convex, and the convex form a subset of the proper. Propriety is introduced to limit the figures to "plain old" polygons.

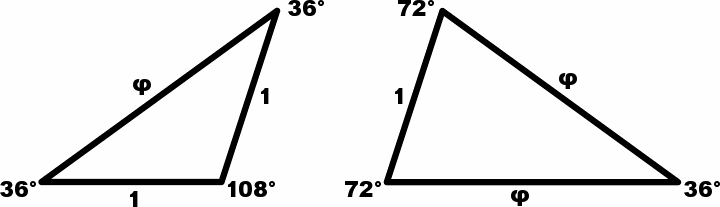
The side-length ratio φ and the 36° angle go hand in hand, as illustrated by the following two well-known triangles:

The area of the larger triangle (0.769421) is φ times the area of the smaller (0.475528).

While the non-convex deciphis are infinite in number, there are precisely 98 convex deciphis, listed in the table below. Each of these figures is assigned an arbitrary three-digit model number for convenience of reference, and all are drawn to the same scale.

If a polygon has axes of reflective symmetry, one of them is drawn vertically to make the symmetry more obvious. Polygons lacking an axis of symmetry form mirror-image pairs which are drawn in the same compartment of a table. Their model numbers can be notated with a double-ended arrow, for instance 406 ↔ 407.

Below each polygon is given its area in terms of a = ½ cos 18° and b = ½ cos 54°. This a & b notation also aids in determining how a larger convex deciphi might (or might not) be partitionable into smaller convex deciphis. Below each area is then given the polygon's perimeter. There are important even-odd relationships among these:

area		perimeter		number of sides
coefficient of a	coefficient of b	integer	coefficient of φ
even	even	even	even	even
even	odd	odd	odd	even
odd	odd	odd	even	odd
odd	even	even	odd	odd

Equilateral polygons are shown on a yellow background; there are seven in each of the two side lengths.

A diagonal of a polygon is shown if the angle it forms with an edge is a multiple of 36°. The length of such a diagonal equals an integer added to an integral power of φ. The lengths of other diagonals are not easy to characterize.

Two elementary properties of n-gons when n is even:

• If any polygon has 180° rotative symmetry, opposite sides must be parallel.
• If any polygon has 180° rotative symmetry, opposite sides must be the same length.

Tiles can be manufactured in these shapes as an educational toy. Few sets would include all 98 polygons; the youngest children might benefit from a set limited to equilateral polygons.

3-gons	one axis of reflective symmetry: a 2 + φ a + b 1 + 2φ same sequence of angles: none same sequence of sides: none
4-gons	180° rotative symmetry, two axes of reflective symmetry: 2b 4 2a + 2b 4φ 2a 4 4a + 2b 4φ one axis of reflective symmetry: 2a + 2b 2 + 2φ 2a + b 3 + φ 180° rotative symmetry: 2a 2 + 2φ 2a + 2b 2 + 2φ same sequence of angles: 400, 401, 406, 407 402, 403, 408, 409 same sequence of sides: 400, 402 401, 403 406, 407, 408, 409 same both: 406, 407 408, 409
5-gons	72° rotative symmetry, five axes of reflective symmetry: 3a + b 5 7a + 4b 5φ one axis of reflective symmetry: 3a + 3b 3 + 2φ no symmetry: 3a + 2b 4 + 1φ 5a + 2b 2 + 3φ 3a + 3b 3 + 2φ 5a + 3b 1 + 4φ same sequence of angles: 500, 501 503, 505 504, 506 507, 509 508, 510 same sequence of sides: 503, 504 505, 506 507, 508 509, 510
6-gons	180° rotative symmetry, two axes of reflective symmetry: 4a + 2b 6 4a + 6b 4 + 2φ 6a + 6b 2 + 4φ 10a + 6b 6φ 2a + 4b 6 6a 4 + 2φ 8a + 2b 2 + 4φ 8a + 6b 6φ one axis of reflective symmetry: 6a + 2b 4 + 2φ 6a + 6b 2 + 4φ 8a + 4b 2 + 4φ 4a + 4b 4 + 2φ 6a + 5b 3 + 3φ 180° rotative symmetry: 6a + 2b 4 + 2φ 8a + 4b 2 + 4φ 4a + 4b 4 + 2φ 6a + 4b 2 + 4φ no symmetry: 4a + 3b 5 + 1φ 6a + 3b 3 + 3φ same sequence of angles: 600, 601, 602, 603, 613, 614, 615, 616 604, 605, 606, 607, 617, 618, 619, 620 608, 609 621, 623 622, 624 same sequence of sides: 600, 604 601, 605, 613, 614, 617, 618 602, 606, 615, 616, 619, 620 603, 607 608, 611 609, 610 621, 622 same both: 601, 613, 614 602, 615, 616 605, 617, 618 606, 619, 620
7-gons	one axis of reflective symmetry: 5a + 6b 6 + 1φ 7a + 5b 5 + 2φ 9a + 4b 4 + 3φ 11a + 6b 2 + 5φ 13a + 7b 1 + 6φ no symmetry: 7a + 5b 5 + 2φ 9a + 7b 3 + 4φ 9a + 7b 3 + 4φ 9a + 4b 4 + 3φ same sequence of angles: 700, 703, 711, 712 701, 702, 704, 709, 710 705, 707 706, 708 same sequence of sides: 705, 706 707, 708 709, 710 same both: 709, 710
8-gons	180° rotative symmetry, two axes of reflective symmetry: 6a + 6b 8 12a + 6b 4 + 4φ 12a + 8b 4 + 4φ 18a + 12b 8φ one axis of reflective symmetry: 8a + 8b 6 + 2φ 12a + 8b 4 + 4φ 8a + 5b 7 + φ 14a + 7b 3 + 5φ 12a + 8b 4 + 4φ 16a + 8b 2 + 6φ 180° rotative symmetry: 8a + 8b 6 + 2φ 10a + 4b 6 + 2φ 10a + 10b 4 + 4φ 14a + 4b 4 + 4φ 16a + 8b 2 + 6φ 14a + 10b 2 + 6φ no symmetry: 10a + 7b 5 + 3φ same sequence of angles: 800, 801, 802, 803, 810, 811, 812, 813, 814, 815, 816, 817, 818, 819, 820, 821 804, 805 806, 807, 808, 809, 822, 823 same sequence of sides: 801, 802, 814, 815 810, 811, 812, 813 816, 817 818, 819, 820, 821 same both: 801, 802, 814, 815 810, 811, 812, 813 816, 817 818, 819, 820, 821
9-gons	one axis of reflective symmetry: 11a + 9b 7 + 2φ 17a + 13b 3 + 6φ no symmetry: 15a + 9b 5 + 4φ same sequence of angles: all same sequence of sides: none
10-gons	To save space, the prefix for the model number is 1- and not 10-. 36° rotative symmetry, ten axes of reflective symmetry: 10a + 10b 10 30a + 20b 10φ 72° rotative symmetry, five axes of reflective symmetry: 22a + 9b 5 + 5φ 180° rotative symmetry, two axes of reflective symmetry: 14a + 10b 8 + 2φ 20a + 8b 6 + 4φ 16a + 14b 6 + 4φ 26a + 16b 2 + 8φ 24a + 10b 4 + 6φ 20a + 16b 4 + 6φ same sequence of angles: all same sequence of sides: none

The polygons can be sorted by area:

approx exact polygons 0.47553 a 300 0.58779 2b 400 0.76942 a + b 301 0.95106 2a 402, 406 ↔ 407 1.24495 2a + b 405 1.53884 2a + 2b 401, 404, 408 ↔ 409 1.72048 3a + b 500 2.01437 3a + 2b 503 ↔ 504 2.12663 2a + 4b 604 2.30826 3a + 3b 502, 507 ↔ 508 2.48990 4a + 2b 403, 600 2.78379 4a + 3b 621 ↔ 622 2.85317 6a 605 2.96543 5a + 2b 505 ↔ 506 3.07768 4a + 4b 611, 617 ↔ 618 3.25932 5a + 3b 509 ↔ 510 3.44095 6a + 2b 608, 613 ↔ 614 3.66547 4a + 6b 601 3.73485 6a + 3b 623 ↔ 624

approx exact polygons 4.02874 6a + 4b 619 ↔ 620 4.14100 5a + 6b 700 4.32263 6a + 5b 612 4.39201 8a + 2b 606 4.50427 7a + 4b 501 4.61653 6a + 6b 602, 609, 800 4.79816 7a + 5b 701, 705 ↔ 706 4.97980 8a + 4b 610, 615 ↔ 616 5.27369 8a + 5b 806 5.45532 9a + 4b 702, 711 ↔ 712 5.56758 8a + 6b 607 5.93085 10a + 4b 812 ↔ 813 6.15537 8a + 8b 804, 810 ↔ 811 6.33700 9a + 7b 707 ↔ 708, 709 ↔ 710 6.51864 10a + 6b 603 6.81253 10a + 7b 822 ↔ 823 6.99417 11a + 6b 703

approx exact polygons 7.46969 12a + 6b 801 7.69421 10a + 10b 814 ↔ 815, 100 7.83297 14a + 4b 816 ↔ 817 7.87584 11a + 9b 900 8.05748 12a + 8b 802, 805, 808 8.23912 13a + 7b 704 8.71464 14a + 7b 807 9.59632 14a + 10b 820 ↔ 821, 103 9.77796 15a + 9b 902 ↔ 903 9.95959 16a + 8b 809, 818 ↔ 819 11.72295 16a + 14b 105 11.86171 20a + 8b 104 11.90458 17a + 13b 901 12.08622 18a + 12b 803 13.10666 22a + 9b 102 14.21285 20a + 16b 108 14.35160 24a + 10b 107 17.06602 26a + 16b 106 20.14370 30a + 20b 101

Here is a sample tessellation:

Related are the penrose tilings, which were developed in a search for aperiodic tessellations.

A related discussion.