
Return to page one.
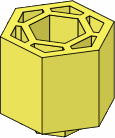
A significantly different, but compatible, kind of brick can now be introduced. These new bricks are termed lateral, in contrast to the punctual bricks detailed in sections A, B and C above. The rationale for these adjectives will be given at figure D-8 below.
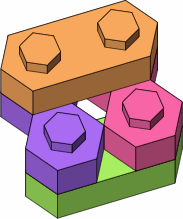
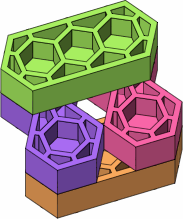
In figure D-1 two lateral bricks are drawn in green and orange; purple and magenta punctual bricks, the same as in figure C-3, form a basis of comparison.
| D-1 |   
|
|---|
Figure D-2 shows the substantial difference between a four-stud lateral brick (orange) and a four-stud punctual brick (blue). The one-stud bricks were added to the drawing to suggest a rectangular grid that underlies the design, while figure D-2c adds an overlay showing an underlying hexagonal grid that is not disturbed whether the bricks are lateral or punctual.
| D-2a | 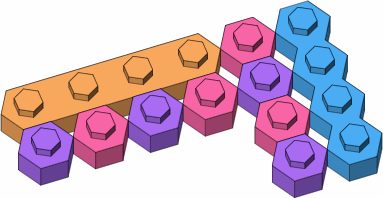
|
|---|---|
| D-2b | 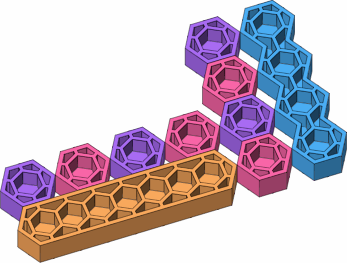
|
| D-2c | 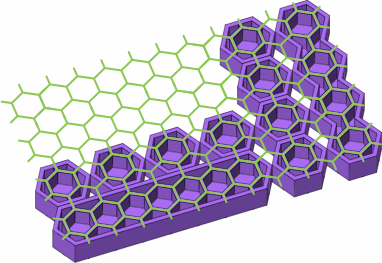
|
If long punctual bricks are attached to each other (figure D-3a), they will either be at a 60-degree angle or be parallel; the same can be said for long laterals (figure D-3b). The figure also emphasizes how multi-stud punctual bricks will have corrugated sides, while lateral bricks will have smooth sides.
| D-3a punctual | 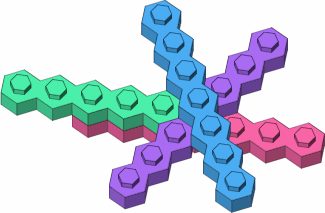
|
| D-3b lateral | 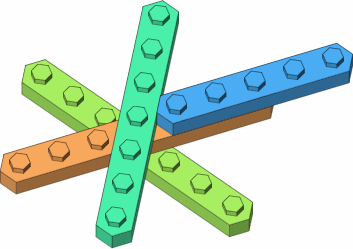
|
A long punctual brick can be attached to a long lateral brick at 90 degrees, as in figure D-4.
| D-4 | 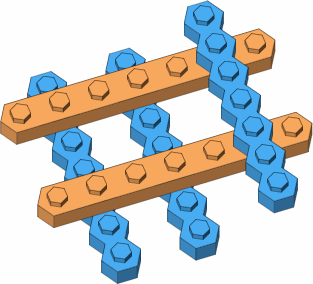
|
|---|
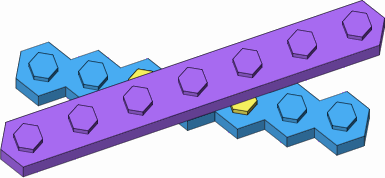
Figure D-5 shows the attempt to attach a long punctual brick to a long lateral brick at a 30-degree angle. This ordinarily fails (figure D-5a) because the wall of the upper brick collides with studs (highlighted in yellow) of the lower brick. It does succeed in the one case where the bricks are attached end to end (figure D-5b).
| D-5a general case, not successful | 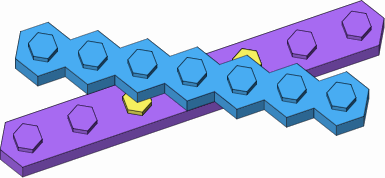
|
| D-5b special case, successful | 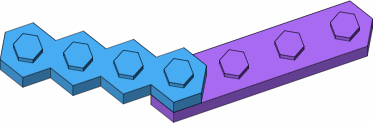
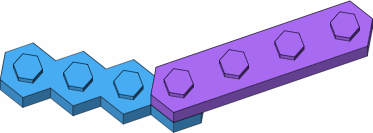
|
Viewing from a different angle, figure D-6a displays a workaround where a single-stud brick (orange) provides vertical clearance that eliminates the conflict of figure D-5a. Figure D-6b reveals that there is precisely enough horizontal clearance to further install two pillars of single-stud bricks.
| D-6a | 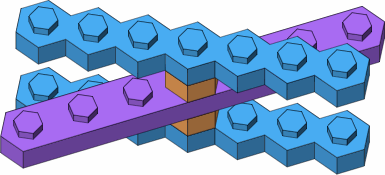
|
|---|---|
| D-6b | 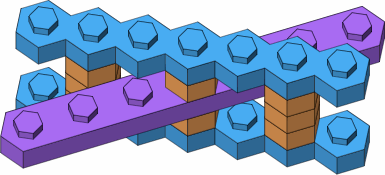
|
The brick in figure D-7, although valid, does not fall cleanly into either of the punctual or lateral categories.
| D-7 | 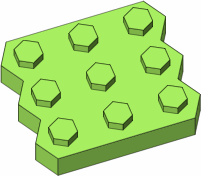 
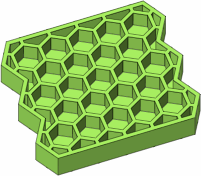
|
|---|
Figure D-8 shows two two-stud bricks, one lateral (purple) and the other punctual (blue), with some yellow highlights. On the lateral brick, the studs face each other side to side; on the punctual, point to point. This explains the names.
| D-8 | 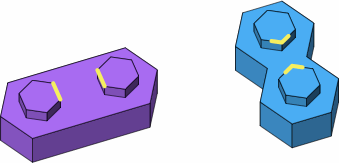
|
|---|
Figure D-9 is the lateral equivalent of the punctual wall of figure A-8a. All the walls and bricks of section A similarly have lateral equivalents.
| D-9 | 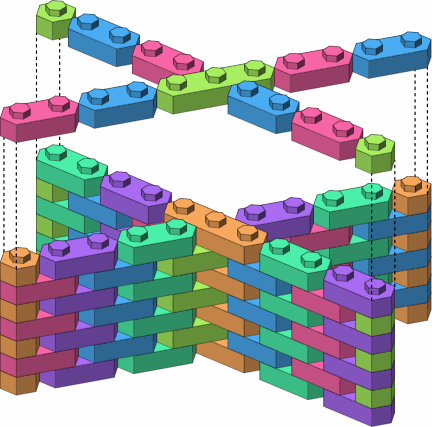
|
|---|
With lateral bricks, unlike punctuals, the pattern of bricks in a wall will be conspicuous even if they are all the same color (figure D-10).
| D-10 | 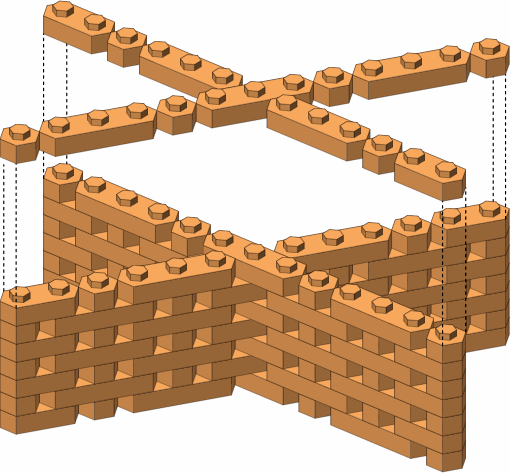
|
|---|
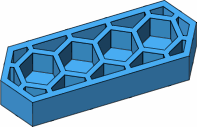
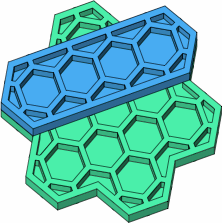
A stretched lateral brick is also possible, as drawn in blue in figure D-11a; an ordinary lateral brick is drawn in orange for comparison. Figure D-11b shows how this stretched brick fits the seven-stud brick of figure C-2. Because the studs of this blue brick fit into sockets that are directly underneath the studs of the green brick, the blue brick can be described as having been placed in phase.
| D-11a |
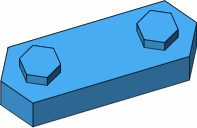 
|
|---|---|
| D-11b |
|
A lateral brick with at least two studs offers at least one socket for out-of-phase connection; in this regard laterals are somewhat more flexible than punctuals. However, when lateral and punctual bricks are used together, the distinction between the terms in-phase and out-of-phase becomes muddled.
Figure E-1 is like figure C-2 except that the bricks's outer wall has been taken away and the symbolic colorations are gone. Besides eliminating the stud-wall collision problem of figure D-5a, this removal weakens the distinction between in-phase and out-of-phase placement. Without the outer wall to add strength, however, the brick might be more subject to accidental breakage.
| E-1 | 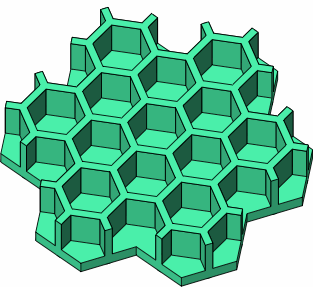
|
|---|
Figure E-2 shows this brick from the top.
| E-2 | 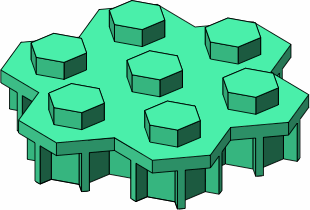
|
|---|
In figure E-3 are simple structures using bricks that lack the outer wall. Although the results look complicated, these bricks are no more difficult to use than those bricks that retain the outer wall.
| E-3a punctual | 
|
| E-3b lateral | 
|
In figure E-4, the blue brick's lack of outer wall is essential in allowing it to fit on top of the green brick, as an outer wall would collide with green studs. One of the blue studs is directly over a green stud; the other is not.
| E-4 | 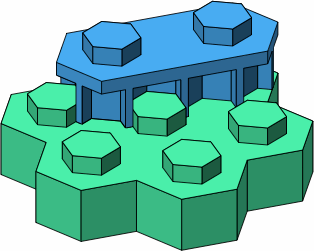
|
|---|
In general, bricks that have the outer wall can be combined freely with bricks that do not.
Little has been said thus far about exactly how big these bricks are going to be, because a wide variety of sizes will work as long as the bricks within a set are consistent. Figure F-1 establishes some terminology with over and under views of two bricks.
| F-1a | 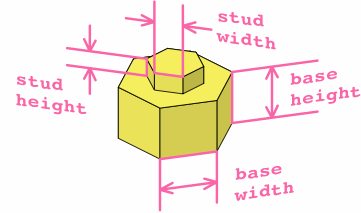
|
|---|---|
| F-1b cutaway | 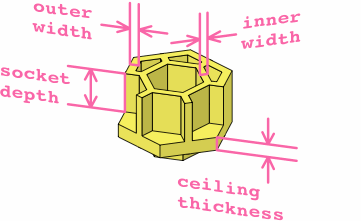
|
Incidentally, figure F-1b presents a valid brick that has outer walls on some partial sockets but not others.
Likely measurements for the base height and the base width are between 6 and 12 millimeters. The two values need not be equal, although they happen to be rendered that way in the drawings above. Figure F-2 shows two variations on their ratio.
| F-2 |   
|
|---|---|
|
More comments on dimensions:
Some manufacturers might prefer a round stud (figure F-3a). For a crisp fit in the hexagonal sockets, the diameter should be √3 (approximately 1.732) times the stud width as given in figure F-1a. Figure F-3b shows how this diameter equals the distance "across flats" of the hexagonal stud.
| F-3a | 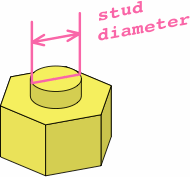
| F-3b | 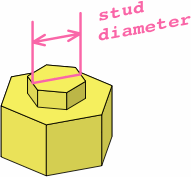
|
|---|
When single-stud bricks have round studs, the bricks can be rotated to arbitrary angles (figure F-4). Opinions may vary on whether this is advantageous or detrimental.
| F-4 | 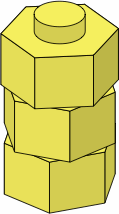
|
|---|
Similarly, if the bricks in the wall of figure E-3b (but not E-3a) have round studs, the wall can curve.
Figure F-5, taken from figure D-2a, suggests how to obtain the dimensions of multiple-stud punctual or lateral bricks. The overall shape of the punctual brick is simply the union of the singles, but the lateral has additional regions filled in.
| F-5 | 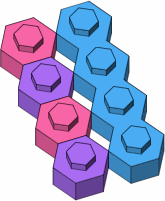  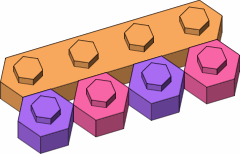
|
|---|
Most systems of children's toy bricks are rectangular, and it is possible to devise a conversion brick to connect the rectangulars to the hexagonals (figure G-1).
| G-1 | 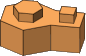
|
|---|
Figure G-2 employs the conversion brick in a simple application.
| G-2 | 
|
|---|
However, it will generally be difficult to design a complicated structure where rectangular and hexagonal bricks are extensively mixed. This is because in a triangle containing angles of 30, 60 and 90 degrees, the length of the longer leg is irrational relative to the length of hypotenuse or shorter leg.
Colophon. This page was prepared on an Apple Macintosh running OS X. The html was written with an ordinary text editor, but the images were a little more complicated:
Return to page one.