home page (§1-2-3) — introduction and rules
next page (§7-8-9) — miscellaneous variations

§4. The following examples, assuming a modulus of eleven, show some ways that sequences can be installed on the board.

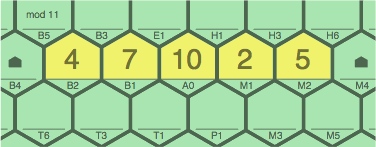
Figure 4A is an example of what the first player might do in their first turn. Although it would be legal to make a sequence of only one or two tiles, most players will try to do something that earns a score. This five-tile sequence is worth 6 points.

figure 4A using 4B2, 7B1, 10A0, 2M1, 5M2

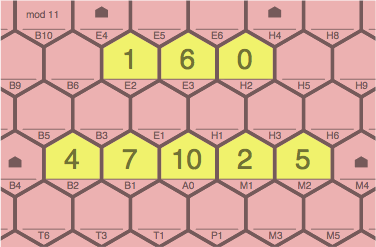
Figure 4B is ILLEGAL (with a red board to emphasize) as a second turn because no added tile is adjacent to any tile previously played.

ILLEGAL figure 4B adding 1E2, 6E3, 0H2 to 4A

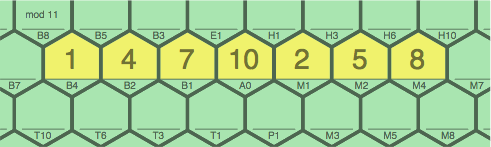
Figure 4C shows extension of the sequence of 4A. If either 1B4 or 8M4 is added, the score is 10 points; if both, the score is 15 points. A player who has the right tiles can extend the sequence further.

figure 4C adding 1B4, 8M4 to 4A

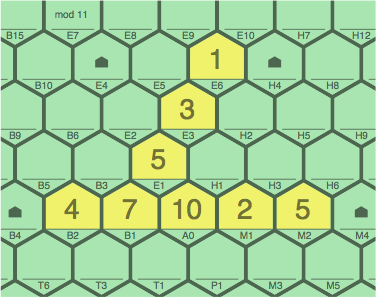
Figure 4D shows another possible second move, branching from a tile in the middle of a previous sequence. The player scores 3 points for their four-tile primary sequence (7B1 ~ 5E1 ~ 3E3 ~ 1E6) even though only three tiles were added. Note the secondary sequence at 5E1 ~ 10A0 (0 points), which some player might extend in a future turn with 0E2 or 4P1.

figure 4D adding 5E1, 3E3, 1E6 to 4A

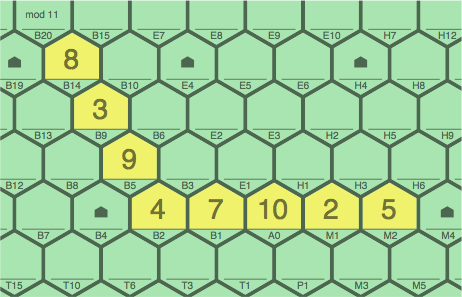
In figure 4E, an added sequence branches off a tile at the end of a sequence. Had the play instead been 9B3 ~ 3E2 ~ 8E5, a secondary sequence of length two would have appeared at 9B3 ~ 7B1. Either way, 3 points are earned.

figure 4E adding 9B5, 3B9, 8B14 to 4A

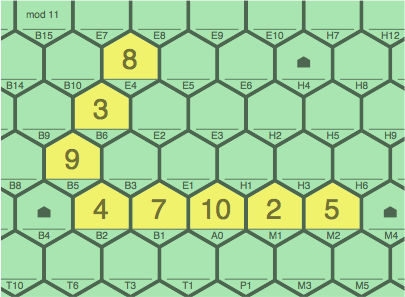
The added tiles in figure 4F earn 1 point for 8E4 ~ 3B6 ~ 9B5 (primary), but 0 points for 9B5 ~ 4B2 (secondary). Cell B4 is now blocked: the zero-slope sequence requires a 1, but the positive-slope sequence requires a 4.

figure 4F adding 9B5, 3B6, 8E4 to 4A

In figure 4F, an alternate play would have added only 9B5, omitting 3B6 and 8E4. Although legal, it would score zero. Here, 9B5 ~ 4B2 would be the primary sequence.

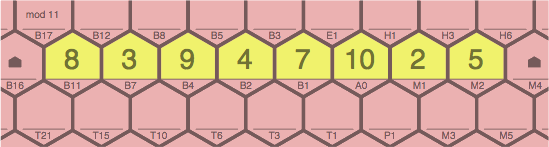
Figure 4G is ILLEGAL because all the tiles are connected and in a straight line, but there is not a constant step size. This eight-tile sequence attempt fails even though 8 ~ 3 ~ 9 ~ 4 and 4 ~ 7 ~ 10 ~ 2 ~ 5 are individually acceptable.

ILLEGAL figure 4G adding 9B4, 3B7, 8B11 to 4A

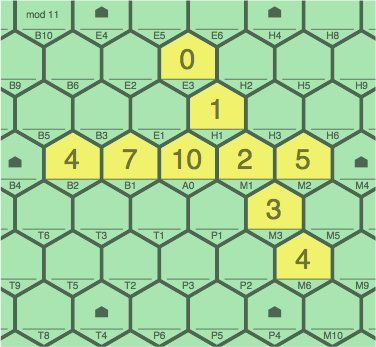
In figure 4H, a new sequence crosses an older one at a tile in the middle (2M1) for six points.

figure 4H adding 0E3, 1H1, 3M3, 4M6 to 4A

Figures 4I and 4J demarcate a subtle difference. In 4I, four added tiles cross the previous sequence at the end at 5M2. The score is 6. Not a secondary sequence is 4 ~ 7 ~ 10 ~ 2 ~ 5, because it was not modified.

figure 4I adding 1H2, 3H3, 7M5, 9M9 to 4A

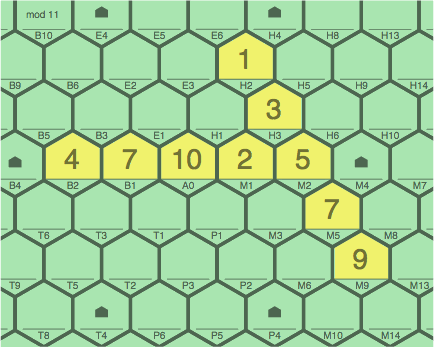
In 4J, five tiles are added, and one of them (8M4) extends the previous sequence. Here, the score is 16 = 6 + 10. Sequence 4 ~ 7 ~ 10 ~ 2 ~ 5 ~ 8 is classified as secondary, because it was extended by a tile added in this turn.

figure 4J adding 0H5, 4H6, 8M4, 1M8, 5M13 to 4A

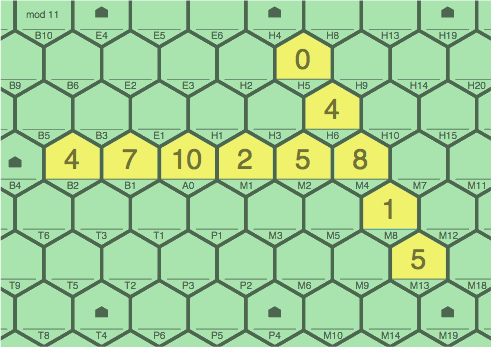
§5. The figures in this section, which assume a modulus of twelve, show what can happen when one sequence is installed next to another.

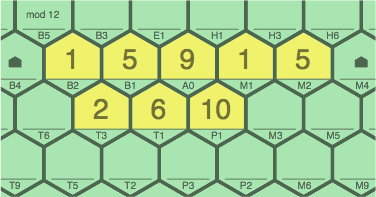
Figure 5A is a possible first play, scoring 6 points.

figure 5A using 1B2, 5B1, 9A0, 1M1, 5M2

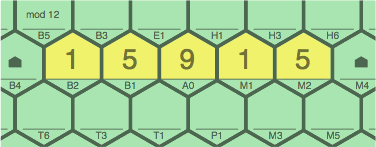
Figure 5B adds 2T3 ~ 4T1 ~ 6P1 to earn 1 point. This leads to blockage of cells E1, T2, and T3:

• 2T3 ~ 5B1 ~ 8∗E1 versus 6P1 ~ 9A0 ~ 0∗E1
• 1B2 ~ 2T3 ~ 3∗T2 versus 9A0 ~ 4T1 ~ 11∗T2
• 5B1 ~ 4T1 ~ 3∗P3 versus 1M1 ~ 6P1 ~ 11∗P3

figure 5B adding 2T3, 4T1, 6P1 to 5A

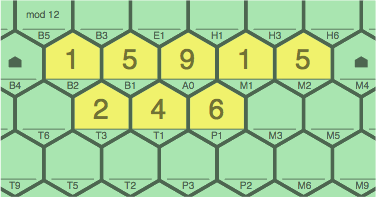
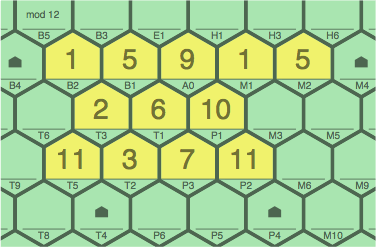
A different addition in figure 5C (still 1 point) does not block anything:

figure 5C adding 2T3, 6T1, 10P1 to 5A

In figure 5D, the next player takes advantage of the lack of blocking; scoring 9 points, calculated as 3 points for this primary sequence of four:

• 11T5 ~ 3T2 ~ 7P3 ~ 11P2

• 11T5 ~ 2T3 ~ 5B1
• 3T2 ~ 6T1 ~ 9A0
• 7P3 ~ 10P1 ~ 1M1
• 3T2 ~ 2T3 ~ 1B2
• 7P3 ~ 6T1 ~ 5B1
• 11P2 ~ 10P1 ~ 9A0

figure 5D adding 11T5, 3T2, 7T3, 11P2 to 5C

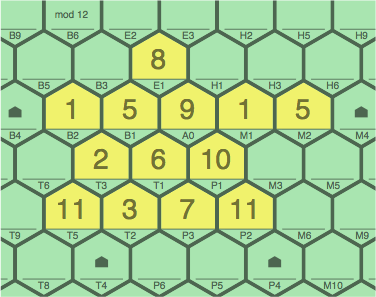
In figure 5E the next player earns 6 points for extending two sequences into four tiles each: 11T5 ~ 2T3 ~ 5B1 ~ 8E1 and 11P2 ~ 10P1 ~ 9A0 ~ 8E1. Either might be deemed primary with the other secondary, if it makes a difference.

figure 5E adding 8E1 to 5D

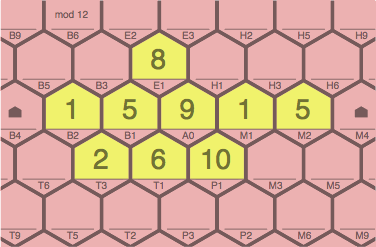
It is ILLEGAL to add — in one turn — the four tiles of figure 5F to the tiles of figure 5A, because cell E1 does not lie in the same straight line as T3 ~ T1 ~ P1.

ILLEGAL figure 5F adding 2T3, 6T1, 10P1, 8E1 to 5A

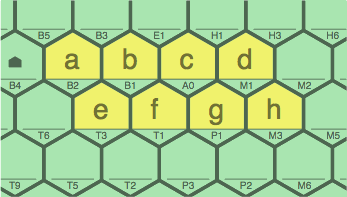
Any two tiles form a valid sequence. As a result, any two sequences may be placed next to each other, parallel, and the combination is valid as long as there is no interference from other sequences. For example in figure 5G appear a ~ b ~ c ~ d and e ~ f ~ g ~ h which, individually considered, can be any two legal sequences. There is no particular relationship between them, but everything still works.

figure 5G

If a ~ b ~ c ~ d and e ~ f ~ g ~ h have the same step size (when reckoned in the same direction), cells B5, B3, E1, H1, T2, P3, P2, and M6 will not be blocked. On the other hand, if the two sequences have differing step sizes, these cells are likely to be blocked.

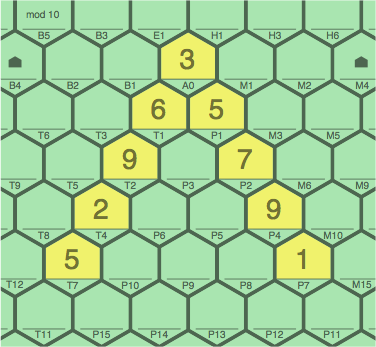
§6. This section looks at filling gaps with examples of modulus 10. After two or more players have taken turns, the board might appear as in figure 6A.

figure 6A

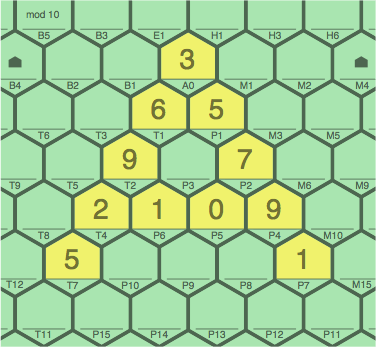
Figure 6B fills the T4 ~ P6 ~ P5 ~ P4 gap in the only manner (3 points). 3T8 and 8M10 could have been appended for a higher score.

figure 6B adding 1P6, 0P5 to 6A

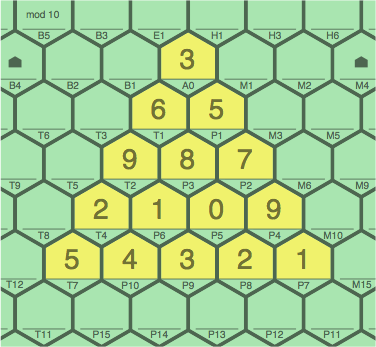
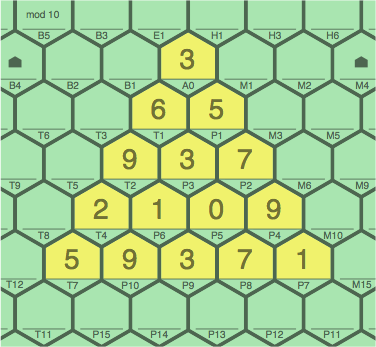
Figures 6C and 6D, each showing tiles added in two turns, show how a dense network can be formed; secondary sequences abound. They also illustrate how there is often more than one way to fill a gap.

figure 6C in one turn adding 8P3 to 6B; in a later turn adding 4P10, 3P9, 2P8		figure 6D in one turn adding 3P3 to 6B; in a later turn adding 9P10, 3P9, 7P8

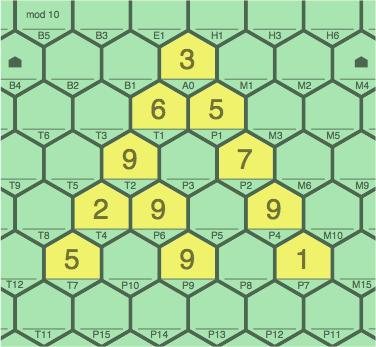
Figure 6E might be the work of a player who prefers that subsequent players not be able to fill gaps. Blocked are cells P5, P3, and T3; but P8 and P10 are still usable.

figure 6E adding 9P6, 9P9 to 6A

next page (§7-8-9) — miscellaneous