
home page (§1-2-3) — introduction and rules
previous page (§4-5-6) — examples
next page (§10) — fibonacciësque variation
§7-1. A variation is to include a few wild tiles among the others. A wild tile does not have a predetermined numerical value, but instead stands for whatever number is specified by the player who installs it on the board in their turn (unless the players have agreed to another method of resolution). That number will not change for the remainder of the game.
The tile might might carry a special symbol or be blank, as in figure 7A. The present discussion employs the hash.
| figure 7A |

|
The number chosen by the player must of course conform to the rules for forming a sequence. For instance, in 2 ~ 5 ~ # ~ 11, the wild tile cannot be anything except an 8. Any sequence that intersects this one must respect that value.
A sequence is permitted to have more than one wild tile, so that 1 ~ # ~ # ~ 7 ~ 9 and # ~ 5 ~ 6 ~ # are acceptable.
For scoring, a wild tile is ignored when calculating the length of a sequence. For instance, 2 ~ 4 ~ 6 ~ 8 ~ 10 (length 5) scores 6, but 2 ~ 4 ~ # ~ 8 ~ 10 (length 4) is worth only 3 points. If 4 ~ 8 ~ 1 (modulus 11) is already on the board, a player can extend it into 4 ~ 8 ~ 1 ~ #, but will earn only one point in doing so.
Wild tiles are most likely to give interesting results when the modulus is large, and the number of tiles in each hand is small.
The distinguishing term for a non-wild tile is natural.
§7-2. Here is a modulus-12 illustration of a problem that might occur with wild tiles. In the sequence 7 ~ # ~ 9, the wild tile might represent either 8 or 2, so the player who installs it declares it to be an 8. Later in the game an honest player erroneously recalls that the wild tile stands for a 2 — or a crooked player engages in trickery — and a dispute ensues. What can be done about this? Here are five possibilities:
A. Suggestion for beginners: Any wild tile, when added to the board, must be an element of a sequence that contains at least two adjacent naturals. This will define the value of the wild tile uniquely, and make its recalculation easy should someone forget.
B. When the modulus is a prime number, more flexible is the following policy: Any wild tile, when added to the board, must be an element of a sequence that contains at least two naturals, but they need not be adjacent. Again, unicity is ensured.
C. Advanced players may prefer this: A wild tile can be added to the board if, by any means under the entire body of rules, that wild tile can be demonstrated to have a unique value. A drawback of this policy is that determination of unicity can be complicated and time-consuming. Under this rule, there is no specific requirement that the sequence contain a particular quantity of natural tiles, or that they be adjacent.
D. An altogether different method of resolving ambiguity is to write down, with pencil and paper for all to see, the declared value of a wild tile. In this case there is no necessity that any incorporating sequence contain any naturals.
E. Finally, some players may prefer to allow ambiguities, leaving them unresolved until, on a subsequent turn, some player installs tiles that settle the value.
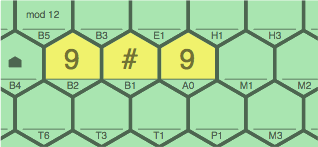
§7-3. Figure 7B, with a modulus of 12, displays an ambiguity, as cell B1 could legally contain either a 3 or a 9. Under optional rule E, the player who installs the wild tile does not declare what number it stands for, instead allowing the uncertainty to remain for an indefinite amount of time. Later, if some player later installs a 3 on cell M1, then B1 will have to be regarded as a 3 (M12-S6-A3); if instead M1 gets a 9, B1 must stand for a 9 itself (M12-S0-A9).
| figure 7B |
|
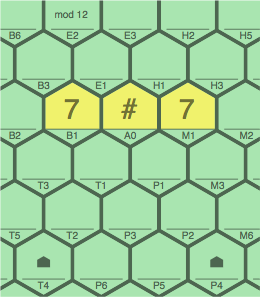
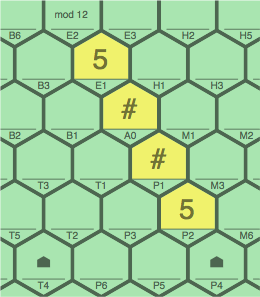
Continuing with a modulus of 12, figures 7C, 7D, and 7E below show how a wild tile ambiguity might be resolved by a broader context. Of interest is cell A0.
If 7C is considered by itself, there are two possibilities:
If 7D is considered by itself, there are three possibilities:
| figure 7C
one of these: A0 = 1 A0 = 7 | figure 7D
one of these: A0 = 9 and P1 = 1 A0 = 5 and P1 = 5 A0 = 1 and P1 = 9 | |
| 
|
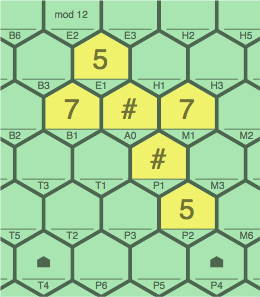
Combined (figure 7E), the only common value for A0 is 1, meaning further that P1 must be 9.
| figure 7E
A0 = 1 and P1 = 9 |
|
§7-4. Some groups of players may agree to allow the hash swap.
A player may, in their regular turn, exchange (one for one) wild tiles on the board with natural tiles from their hand, but all activity must lie within the primary sequence. Specifically, wilds go form board to hand; naturals go from hand to board.
The incoming natural tile must agree with whatever the value of the outgoing wild tile would have been. If playing under the rule allowing the wild to be ambiguous, the natural must agree with some legal value that the wild could have taken.
If a player is replacing multiple ambiguous wild tiles, they must be consistent. Consider 1 ~ # ~ # ~ 4 (modulus 15). Three correct full naturalizations are 1 ~ 2 ~ 3 ~ 4, 1 ~ 7 ~ 13 ~ 4, and 1 ~ 12 ~ 8 ~ 4. Although 1 ~ 2 ~ # ~ 4 and 1 ~ # ~ 13 ~ 4 are valid partial naturalizations, they cannot be combined into 1 ~ 2 ~ 13 ~ 4 because that result is not modular-linear.
When replacing wild tiles, the player may also extend either or both ends of the primary sequence with natural or wild tiles, including any wild tiles liberated earlier in that turn. A wild tile that so moves within a sequence is not required to retain its old value. For instance, a player who holds a 3 and a 7 can convert 1 ~ 2 ~ # ~ 4 ~ 5 into 1 ~ 2 ~ 3 ~ 4 ~ 5 ~ # ~ 7, employing the same wild tile.
Any wild tiles that the player retrieves but does not use in this turn remain in the player's hand for use in future turns, and are not restricted to any previous value they might have borne.
The player scores for the primary sequence, and every secondary sequence in which a wild tile was replaced with a natural. Note that a sequence like 1 ~ 3 ~ # ~ 7 (length 3) would have scored 1 point before the hash swap; but would score 3 points afterward, because it has become of length 4: 1 ~ 3 ~ 5 ~ 7.
The player also scores for every secondary sequence that was formed or extended by any natural or wild tiles used to extend the primary sequence.
In figure 7E, if for example #A0 is replaced with 1A0, the player scores 2, for two sequences of length 3: 7 ~ 1 ~ 7 and 5 ~ 1 ~ # ~ 5.
§8. Optionally, a MODLINSEQ set can contain one special tile for each possible modulus within a practical range, such as in figure 8A. The color of these must contrast with that of the regular tiles.
| figure 8A |

|
When players have agreed on a modulus before play begins, any player takes the appropriate modulus marker and installs it on cell A0. It aids when someone forgets what the modulus is. Other modulus markers will not enter play.
In forming sequences, it is treated exactly the same as a 0, and transcribed 0A0. As always, the first player's first move must incorporate cell A0 in whatever sequence is formed; the difference now is that this first sequence will invariably contain a 0. Sequences formed or extended later will continue to regard the modulus marker as an ordinary 0A0.
As examples, the sequences in figure 8B (modulus 13) are interpreted as 7 ~ 10 ~ 0 ~ 3 ~ 6 and 4 ~ 0 ~ 9.
| figure 8B |
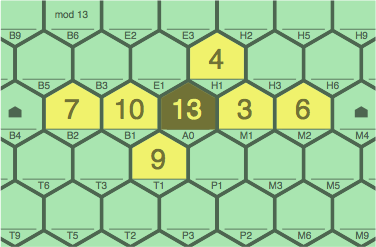
|
§9-1. Some players might want to designate particular cells as awarding a bonus, granting extra points to the player who first installs a tile on each. A suggested pattern for bonus cells (rendered here in white) for an order-6 board is given in figure 9A.
| figure 9A | ||
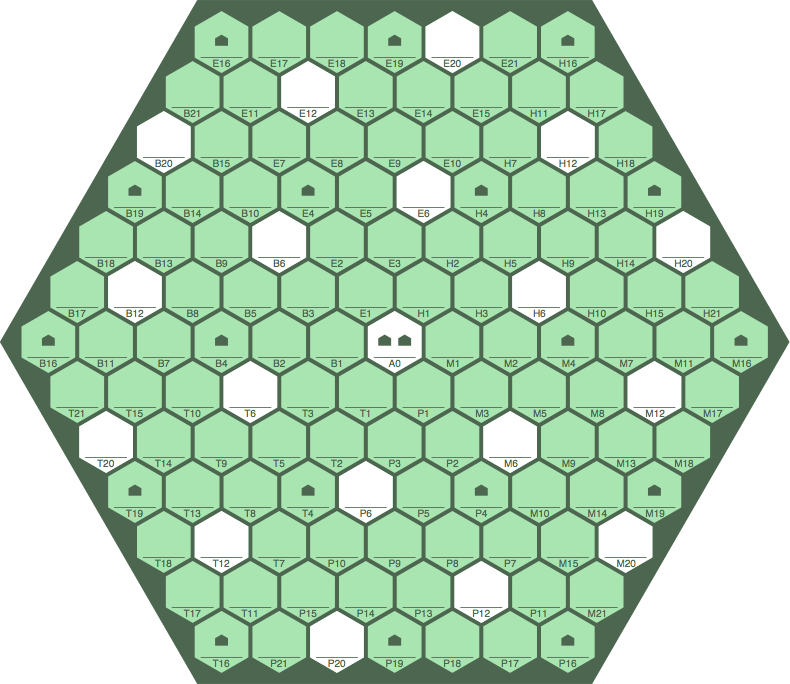
| ||
Bonus cells have the numbers 0, 6, 12, and 20 in their addresses, the same in all sextants of the board. The pattern extends to higher-order boards which would use the numbers 22, 32, 43, 48, 55, 61, 68, 75 as needed.
If figure 9A does not make the arrangement of bonus cells evident, figure 9B below has some lines (not actually printed on the board) which may help: they connect the centers of the bonus cells. On higher-order boards the lines are extended to establish where further bonus cells will be.
| figure 9B | ||
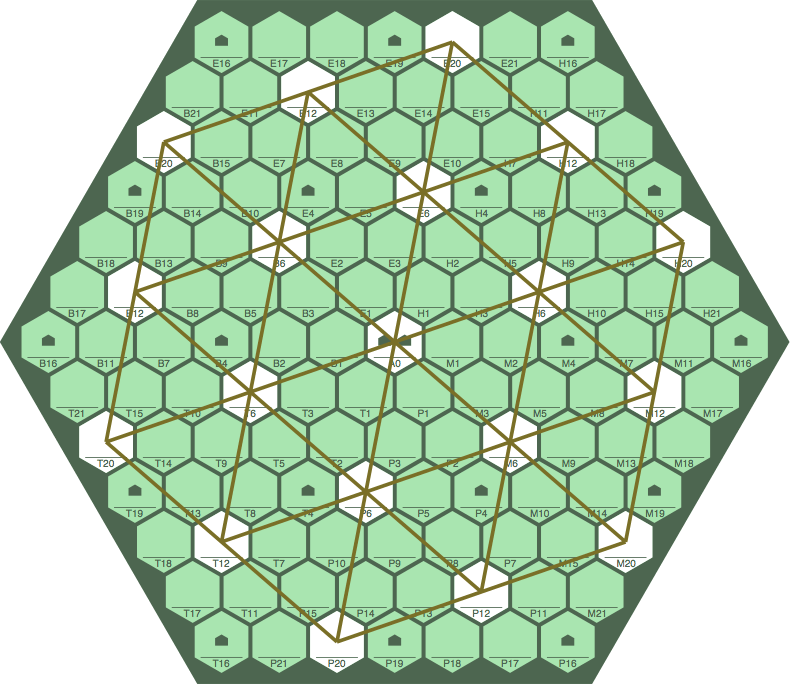
| ||
With boards of at least order 5, approximately 1 of every 7 cells gives a bonus, offering players frequent opportunities to earn extra points. Indeed, every non-bonus cell is adjacent to a bonus cell, except perhaps at the edge of the board. However, the bonus cells are scattered in such a way that a player can hardly monopolize them one one turn. In particular, a sequence would need 8 tiles to cover two bonus cells, or 15 tiles (on a board of order 7 at least) to cover three bonuses.
| table 9A | ||||||
|---|---|---|---|---|---|---|
| order | bonus cells | total cells | order | bonus cells | total cells | |
| 0 | 1 | 1 | 6 | 19 | 127 | |
| 1 | 1 | 7 | 7 | 25 | 169 | |
| 2 | 1 | 19 | 8 | 31 | 217 | |
| 3 | 7 | 37 | 9 | 37 | 271 | |
| 4 | 7 | 61 | 10 | 49 | 331 | |
| 5 | 13 | 91 | 11 | 55 | 397 | |
§9-2. One possible method of calculating a bonus score is this: the player who first installs a tile on a bonus cell adds 1, for scoring purposes, to the length of each sequence that includes that cell. Players who subsequently extend any of these sequences do not benefit from this bonus cell.
When wild tiles are used and the hash swap is permitted, a player who removes a wild tile from a bonus cell and replaces it with a natural also receives the bonus.
§9-3. Another option is to have not only bonus cells, but also malus cells. (From Latin: "bonus" = "good"; "malus" = "bad"). The player who installs a tile on a malus cell has 1 subtracted from the length of their sequence(s) for scoring purposes; this is the opposite of the bonus cell's effect.
Figure 9C shows a possible pattern of bonus ("+") and malus ("−") cells. Because the board is of a high order, this image is at a smaller scale than the others. Also, pentagons are omitted for clarity.
| figure 9C | ||
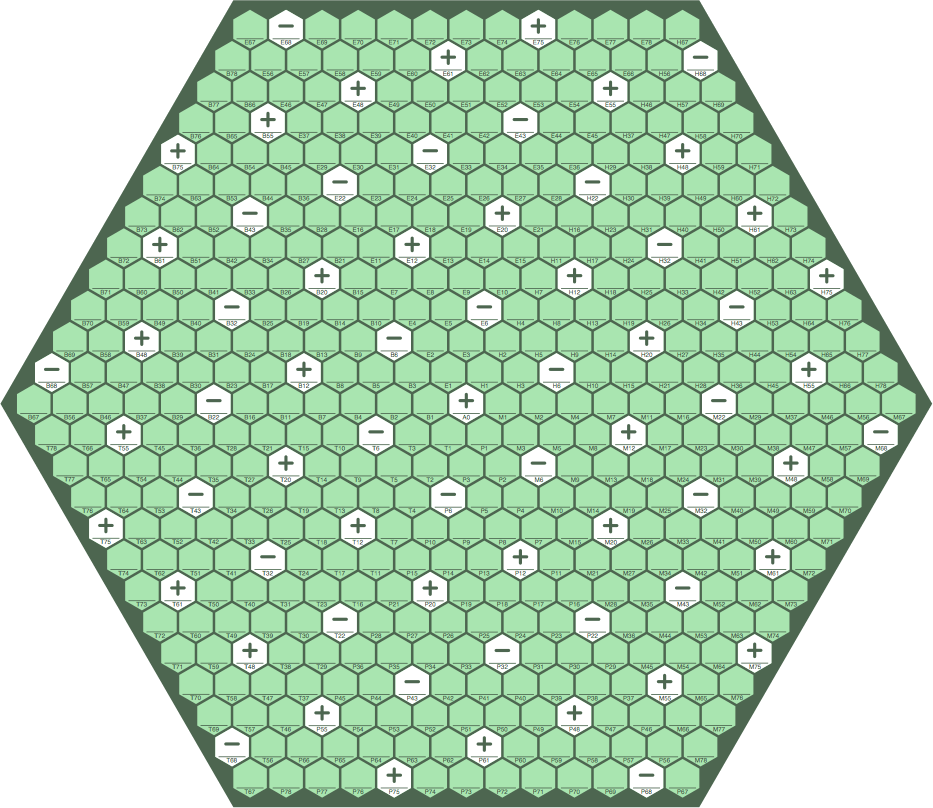
| ||
The bonus and malus cells of this pattern form hexagonal rings:
| table 9B | ||
|---|---|---|
| ring | nature | numbers in addresses |
| 0 | bonus + | 0 |
| 1 | malus − | 6 |
| 2 | bonus + | 12, 20 |
| 3 | malus − | 22, 32, 43 |
| 4 | bonus + | 48, 55, 61, 75 |
| 5 | malus − | 68, 83, 90, 99, 116 |
| 6 | bonus + | 92, 109, 127, 134, 146, 166 |
With a sufficiently long sequence, a player might receive two bonuses; two maluses; or one of each, which would cancel.
next page (§10) — fibonacciësque variation