home page (§1-2-3) — introduction and rules
previous page (§7-8-9) — miscellaneous variations
next page (§11) — multiplicative variation

§10-1. There is an alternative to modular linear sequences, namely modular fibonacciësque sequences (theory).

Although the sequences of §2-4 are modular-linear when reckoned either in either direction, these fibonacciësque sequences have a forward direction and a backward direction. A sequence can be extended both forwards and backwards, but the method of calculation differs a bit.

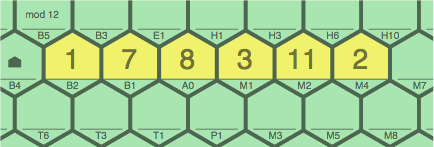
As an introduction, consider the following sequence with a modulus of 12:

figure 10A

There are two equally valid ways of calculating the sequence 1 ~ 7 ~ 8 ~ 3 ~ 11 ~ 2 (compare §2-1):

• Moving left to right, from B2 to M4, add each tile to the previous tile at each step:
  • 1 + 7 = 8
  • 7 + 8 = 15 is not less than the modulus, so subtract the modulus: 15 − 12 = 3
  • 8 + 3 = 11
  • 3 + 11 = 14 is not less than the modulus, so subtract the modulus: 14 − 12 = 2
• Moving right to left, from M4 to B2, subtract each tile from the previous tile at each step:
  • 2 − 11 = −9 is less than zero, so add the modulus: −9 + 12 = 3
  • 11 − 3 = 8
  • 3 − 8 = −5 is less than zero, so add the modulus: −5 + 12 = 7
  • 8 − 7 = 1

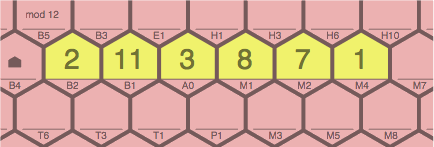
A zero-slope sequence must add to the right and subtract to the left. Figure 10B is ILLEGAL because it does the opposite:

ILLEGAL figure 10B

To prevent mistakes, arrows at the edge of the board are recommended to indicate the directions of addition, as in figure 10C:

	figure 10C

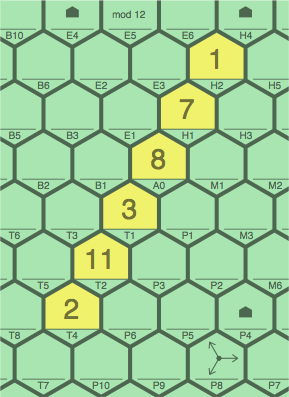
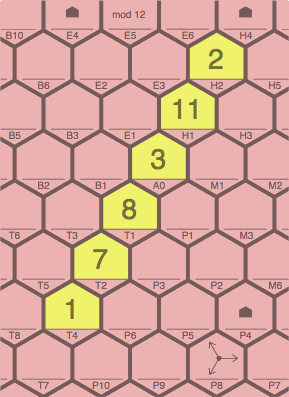
Sequences of positive slope add from upper right to lower left, as in figure 10D. Note in cell P8 the miniature arrows, not actually printed on the board, serving as a reminder of the correct directions of addition.

LEGAL figure 10D		ILLEGAL figure 10E

Sequences of negative slope add from lower right to upper left:

LEGAL figure 10F		ILLEGAL figure 10G

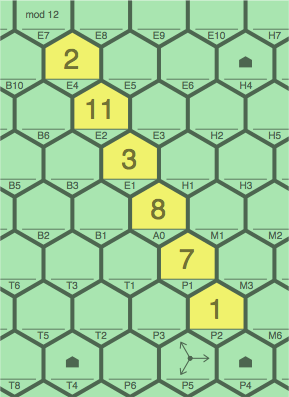
Incidentally, the full sequence from which this example comes has a period of 24:

[ … 6 ~ 5 ~ 11 ~ 4 ~ 3 ~ 7 ~ 10 ~ 5 ~ 3 ~ 8 ~ 11 ~ 7 ~ 6 ~ 1 ~ 7 ~ 8 ~ 3 ~ 11 ~ 2 ~ 1 ~ 3 ~ 4 ~ 7 ~ 11 … ]

Once the modulus is selected, any two numbers define a valid sequence, even if they are two zeros:

[ … 0 ~ 0 ~ 0 ~ 0 ~ 0 … ]

Table 10A is a list of sequences for moduli from 1 through 20.

next page (§11) — multiplicative variation