Page 2 (§4-5-6) — examples
Page 3 (§7-8-9) — miscellaneous variations
Page 4 (§10) — fibonacciësque variation
Page 5 (§11) — multiplicative variation
Page 6 (§12-13-14) — wrap-around variation
Page 7 (§15) — comments

§1-1. MODLINSEQ is a numerical tile-based board game for two or more players.

Players install number-bearing tiles on the board to form sequences, with longer sequences earning substantially greater points. Sequences frequently intersect one another obliquely, ultimately forming a large network of tiles. At the end of the game, the player with the highest score wins.

The name is short for MOD-ular LIN-ear SEQ-uence, which will be explained in §2-4 below.

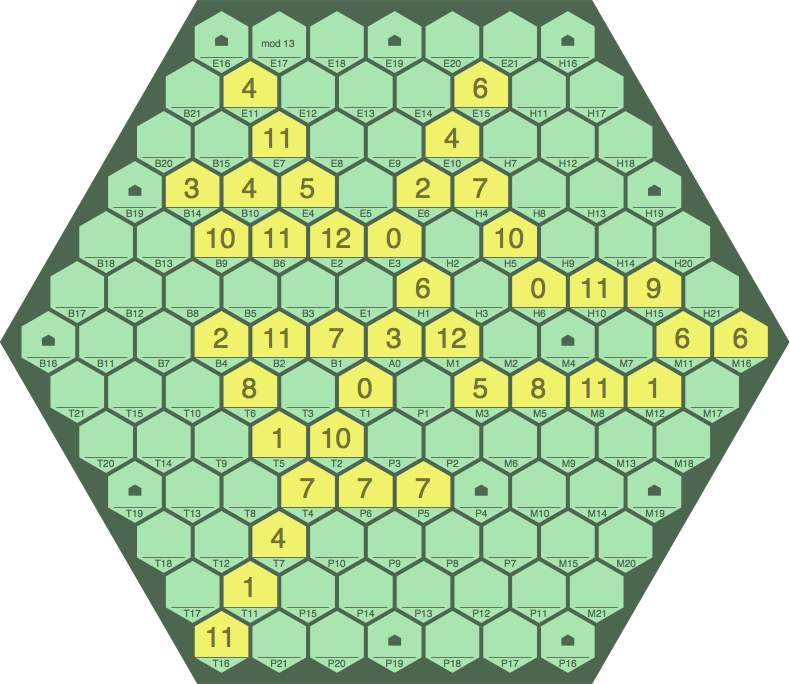
With a green board and yellow tiles, here is what a game in progress could look like:

	figure 1A

Although much detail is provided below, the gist is this: Wherever there is an unbroken straight line of tiles on the board, their numbers must form an arithmetic progression in modular arithmetic — this is called the modular-linear rule. In this example, the modulus is thirteen. Players take turns, installing tiles which extend old sequences, or which create new sequences that intersect old ones.

Many of the images on this page contain an indication of the modulus (as cell E17 in figure 1A) for guidance in case the image is reproduced out of context, which frequently happens on the internet. The modulus number is not actually printed on the board, as it can change from one game to the next as the players desire.

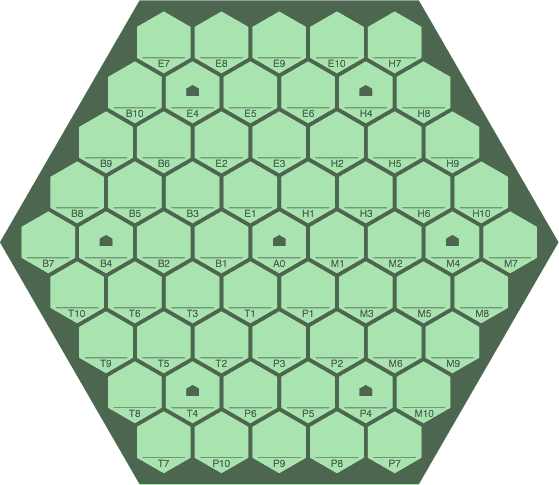
§1-2. The board can be produced in a variety of shapes and sizes. Here is an example without tiles, as at the beginning of a game:

	figure 1B

Although this board has fewer cells than most players would prefer, it still embodies the key properties of a MODLINSEQ board. Essential is that the board be a grid of regular hexagons. Not essential but helpful are the following additional characteristics:

• Each cell contains an address, which is a letter followed by a number. This is for convenience of reference, especially in preparing a transcript of a game.
• Some cells contain a pentagon which makes it easier to count long spans; and to find the center cell A0, which is where play begins. Some cells of a larger board will have multiple pentagons. No rules of the game are dependent on the pentagons.
• Each cell contains a horizontal line which prompts the player to position the tile in the correct direction. Too, the tile when properly installed does not cover the address.

No cell has any distinctive attributes pertaining to how it may be used or how it affects scoring, unless players devise custom rules for particular cells.

Cell addressing starts at the center with cell A0. Cells in the northwest sextant are lettered B, north sextant E, northeast H, southeast M, south P, southwest T. These letters were selected because their glyphs appear in not only the Latin alphabet, but also the Greek and Cyrillic (although pronunciations can differ). This feature facilitates international play.

table 1A
	glyphs chosen							others
Latin	A	B	E	H	M	P	T	K	X
Greek	alpha	beta	epsilon	eta	mu	pi	tau	kappa	chi
Cyrillic	a	ve	ye	en	em	er	te	ka	kha
	Letters O and I are omitted because they can be confused with numerals 0 and 1. Lower-case letters would differ.

Within each sextant, cells are numbered from the center outward. This center-outward addressing scheme offers the best chance of success to the student who has a board of one size and shape, but who has the transcript of a game played on a board of some other size and shape, and who wants to re-enact that game.

While the typical board will have an overall shape of a regular hexagon, such is not absolutely required, as demonstrated by the board in figure 1C that has been truncated (from this) into a shape that is as nearly rectangular as possible. When truncation is performed, cells are simply dropped without adjusting the addresses of those which remain; the usual effect is that some addresses will be skipped over in the final product. The aim is to preserve addressing consistency among boards that are not alike. As a case in point, if each of two different boards has cells addressed as B26 and B20, then B26 will assuredly be to the immediate left of B20 on both boards.

figure 1C

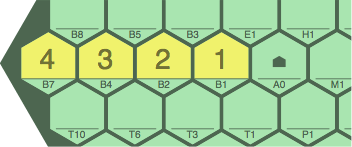
The order of an overall-hexagonal board is the number of cells to the left of A0. An excerpt of figure 1B illustrates how this is to be counted:

figure 1D order 4

Table 1B contains links to images of some boards that have the overall shape of a regular hexagon. Orders 7, 8, and 9 will probably be the most popular. The images are rendered in black and white for the convenience of anyone who wants to customize them.

table 1B images are in the portable document format
order	cells	image		order	cells	image		order	cells	image
0	1	link		7	169	link		13	547	link
1	7	link		8	217	link		14	631	link
2	19	link		9	271	link		15	721	link
3	37	link		10	331	link		16	817	link
4	61	link		11	397	link		17	919	link
5	91	link		12	469	link		18	1027	link
6	127	link		n	3 × n × (n + 1) + 1

Whatever its shape, the board will probably be printed on some sort of heavy paper or cardboard. One color of ink is sufficient.

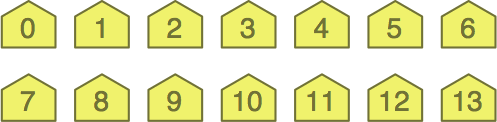
§1-3. A tile, which is of a pentagonal shape, bears a small nonnegative integer on its front, for instance:

figure 1E

The back of each tile is plain, giving no indication of what number is on its front. Each player has a supply of tiles (their hand) whose numbers are not revealed to opponents until the tiles are placed face up on the board in the player's turn.

The tiles might be manufactured thick enough that they stand on edge, like dominoes; or they might be thinner, requiring a rack to hold them. A practical width for a tile is 25 millimeters or 1 inch. Because these tiles do not have rotational symmetry, there is little risk that a player will install a tile on the board in the wrong orientation, mistaking a 6 for a 9.

Before the game, players agree on a modulus, which is a positive integer typically between 8 and 20. The game will then use only those tiles whose numbers are less than the modulus. For example, with a modulus of 15, tiles employed will carry the values 0 through 14. For best results, there should be equal quantities of all the numbers in use.

A feasible set of equipment would furnish ten tiles in each number from 0 to 12. This would allow play with 130 tiles with a modulus of 13; or 120 tiles with a modulus of 12, ten tiles being omitted. Although the rules are the same, game play differs somewhat according to whether the modulus is a prime number (as 13) or not (as 12). A board of order 9 is a good size with this many tiles.

Tiles will likely be manufactured from plastic, although cardboard would suffice as a less durable option.

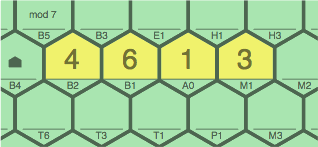
§2-1. Figure 2A is an excerpt of what the board might look like after the first player's first turn in a game with a modulus of 7. Four tiles have been installed.

figure 2A transcript: 4B2, 6B1, 1A0, 3M1

This serves as an introduction to what a modular linear sequence is. Writing the tilde to separate terms within a sequence, there are four equally valid ways of calculating the sequence 4 ~ 6 ~ 1 ~ 3:

• Moving left to right, from B2 to M1, add 2 at each step:
  • 4 + 2 = 6
  • 6 + 2 = 8 is not less than the modulus, so subtract the modulus: 8 − 7 = 1
  • 1 + 2 = 3
• Moving left to right, from B2 to M1, subtract 5 at each step:
  • 4 − 5 = −1 is less than zero, so add the modulus: −1 + 7 = 6
  • 6 − 5 = 1
  • 1 − 5 = −4 is less than zero, so add the modulus: −4 + 7 = 3
• Moving right to left, from M1 to B2, subtract 2 at each step:
  • 3 − 2 = 1
  • 1 − 2 = −1 is less than zero, so add the modulus: −1 + 7 = 6
  • 6 − 2 = 4
• Moving right to left, from M1 to B2, add 5 at each step:
  • 3 + 5 = 8 is not less than the modulus, so subtract the modulus: 8 − 7 = 1
  • 1 + 5 = 6
  • 6 + 5 = 11 is not less than the modulus, so subtract the modulus: 11 − 7 = 4

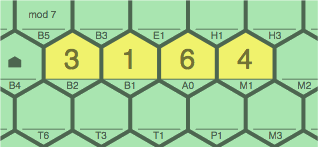
Indeed, we say that 4 ~ 6 ~ 1 ~ 3 and 3 ~ 1 ~ 6 ~ 4 are merely two different notations for the same sequence. Not surprising is that figure 2B is also a correct installation:

figure 2B transcript: 3B2, 1B1, 6A0, 4M1

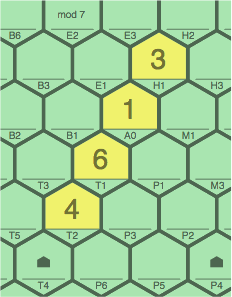
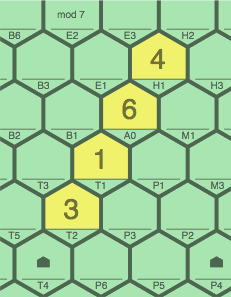
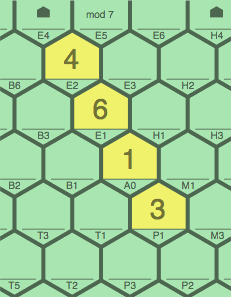
Above, figures 2A and 2B show the sequence placed horizontally (zero slope). It can also be installed as below, in figures 2C and 2D (positive slope); or 2E and 2F (negative slope):

figure 2C transcript: 4T2, 6T1, 1A0, 3H1		figure 2D transcript: 3T2, 1T1, 6A0, 4H1
figure 2E transcript: 4P1, 6A0, 1E1, 3E2		figure 2F transcript: 3P1, 1A0, 6E1, 4E2

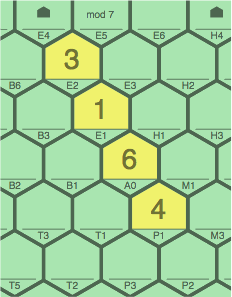
With three different slopes, it frequently happens that one sequence intersects another obliquely.

In the course of a game, players will often extend existing sequences instead of starting new ones; in figure 2E, cell P2 would contain 2 and cell E4 would contain 5. If a sequence is extended far enough, numbers will repeat:

… 3 ~ 5 ~ 0 ~ 2 ~ 4 ~ 6 ~ 1 ~ 3 ~ 5 ~ 0 ~ 2 ~ 4 …

A sequence has no particular maximum length, being extensible until it reaches the edge of the board or encounters a conflicting sequence.

The tilde notation, frequently employed in this report, uses the numbers on tiles as above, or uses cell addresses, or uses both, as convenient:

3 ~ 1 ~ 6 ~ 4
E2 ~ E1 ~ A0 ~ P1
3E2 ~ 1E1 ~ 6A0 ~ 4P1

§2-2. To count as a sequence, the tiles forming it must lie in an unbroken straight line. An additional rule is that whenever there is an unbroken straight line of tiles, they must form a legal (that is, modular-linear) sequence.

Continuing to use modulus 7, figure 2G contains two three-tile sequences, 4 ~ 6 ~ 1 and 1 ~ 3 ~ 5. However, 4 ~ 6 ~ 1 ~ 3 ~ 5 does not qualify as a five-tile sequence because it has a bend. This arrangement could nonetheless arise from legal moves by two players on successive turns.

figure 2G

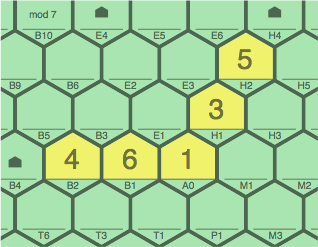
Figure 2H contains two three-tile sequences, 4-6-1 and 5-0-2, which could be connected into a seven-tile sequence by installing a 3 tile on cell M1.

figure 2H

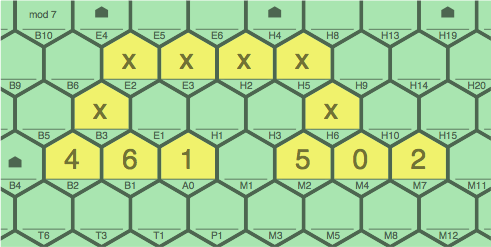
The tiles marked 'x' are necessary because, as play progresses, there can never be two disconnected networks of tiles. These 'x' tiles, which show one of many ways that the two sequences of interest might be connected, do contain genuine numbers in legal sequences; but in this example their exact values happen to be immaterial.

Figure 2I contains two three-tile sequences, 4 ~ 6 ~ 1 and 0 ~ 2 ~ 4, but they can never be connected by way of cell M1, because of a conflict between 4B2 ~ 6B1 ~ 1A0 ~ 3∗M1 and 5∗M1 ~ 0M2 ~ 2M4 ~ 4M7, where the infix asterisk indicates what tile could be installed if there were not a mismatch. M1 is now blocked, remaining vacant for the rest of the game.

figure 2I

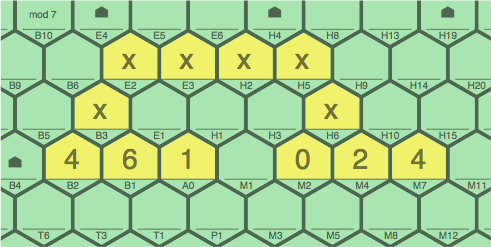
In figure 2J, cell M1 is again blocked for a similar reason: if M1 were to contain 3, M2 would have to contain 5, which it does not.

figure 2J

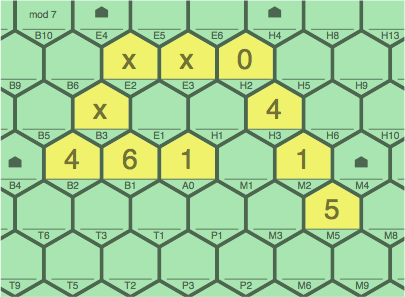
Some players might opt to obtain a supply of red tiles to be placed on blocked cells to conspicuously signify that they are ineligible for further use. A computerized version of MODLINSEQ could detect and mark the blocked cells automatically.

§2-3. The point value of a sequence is based on how many tiles it contains. It grows quadratically to greatly reward the player who can construct long sequences.

table 2A
length	points		length	points
1	0		7	15
2	0		8	21
3	1		9	28
4	3		10	36
5	6		11	45
6	10		12	55
n	(n − 1) × (n − 2) ÷ 2

The reason that a 2-tile sequence counts zero is that no skill or luck is required in producing it: any two tiles, equal or unequal, form a legal sequence. Meanwhile, the sequence of 1 tile is of little more than theoretical interest.

§2-4. There is more to say about sequences, but the player who takes the time to understand them thoroughly has make great strides toward mastery of the game. Among other things, whence comes the name "MODLINSEQ"?

• A sequence is termed modular because calculations "wrap around" when a value would be less than zero; or when a value would not be less than the modulus. In particular, if the result would equal the modulus, it becomes zero.
• A sequence is termed linear because the same number (the step) is added or subtracted each time. The step can even be zero, meaning that a repeated number forms a valid sequence:

  … 3 ~ 3 ~ 3 ~ 3 ~ 3 …

We use the MSA notation to describe a sequence. It consists of:

• 'M' (for modulus), followed by the modulus;
• a hyphen;
• 'S' (for step), followed by a step;
• a hyphen;
• 'A' (for anchor), followed by an anchor.

• The modulus has already been explained.
• The step size usually differs according to whether the sequence is reckoned in one direction or the other. The modulus-7 example in figure 2A could be described with a step size of either 2 or 5; we generally choose the smaller, because a sequence rendered backwards is deemed the same thing as when rendered forwards.
• The anchor can be any number in the sequence, but conventionally is the smallest number that occurs, which is often zero.

§2-5. When the modulus is a prime number, things are fairly simple. In the case of modulus 11 the following are all the possible sequences, and they fall into two obvious categories, as they will for any prime modulus:

table 2B
M11-S1-A0	… 0 ~ 1 ~ 2 ~ 3 ~ 4 ~ 5 ~ 6 ~ 7 ~ 8 ~ 9 ~ 10 …	period = 11		M11-S0-A0	… 0 …	period = 1
M11-S2-A0	… 0 ~ 2 ~ 4 ~ 6 ~ 8 ~ 10 ~ 1 ~ 3 ~ 5 ~ 7 ~ 9 …			M11-S0-A1	… 1 …
M11-S3-A0	… 0 ~ 3 ~ 6 ~ 9 ~ 1 ~ 4 ~ 7 ~ 10 ~ 2 ~ 5 ~ 8 …			M11-S0-A2	… 2 …
M11-S4-A0	… 0 ~ 4 ~ 8 ~ 1 ~ 5 ~ 9 ~ 2 ~ 6 ~ 10 ~ 3 ~ 7 …			M11-S0-A3	… 3 …
M11-S5-A0	… 0 ~ 5 ~ 10 ~ 4 ~ 9 ~ 3 ~ 8 ~ 2 ~ 7 ~ 1 ~ 6 …			M11-S0-A4	… 4 …
because M is prime, "-A0" could be omitted from the notation				M11-S0-A5	… 5 …
				M11-S0-A6	… 6 …
				M11-S0-A7	… 7 …
				M11-S0-A8	… 8 …
				M11-S0-A9	… 9 …
				M11-S0-A10	… 10 …
				because M is prime, "-S0" could be omitted from the notation

For a non-prime number such as 12, there is greater variation in sequences because the modulus is a non-trivial multiple of some step sizes. When that happens, the anchor number becomes essential:

table 2C
M12-S1-A0	… 0 ~ 1 ~ 2 ~ 3 ~ 4 ~ 5 ~ 6 ~ 7 ~ 8 ~ 9 ~ 10 ~ 11 …					period = 12
M12-S5-A0	… 0 ~ 5 ~ 10 ~ 3 ~ 8 ~ 1 ~ 6 ~ 11 ~ 4 ~ 9 ~ 2 ~ 7 …
M12-S2-A0	… 0 ~ 2 ~ 4 ~ 6 ~ 8 ~ 10 …					period = 6
M12-S2-A1	… 1 ~ 3 ~ 5 ~ 7 ~ 9 ~ 11 …
M12-S3-A0	… 0 ~ 3 ~ 6 ~ 9 …	period = 4		M12-S0-A0	… 0 …	period = 1
M12-S3-A1	… 1 ~ 4 ~ 7 ~ 10 …			M12-S0-A1	… 1 …
M12-S3-A2	… 2 ~ 5 ~ 8 ~ 11 …			M12-S0-A2	… 2 …
M12-S4-A0	… 0 ~ 4 ~ 8 …	period = 3		M12-S0-A3	… 3 …
M12-S4-A1	… 1 ~ 5 ~ 9 …			M12-S0-A4	… 4 …
M12-S4-A2	… 2 ~ 6 ~ 10 …			M12-S0-A5	… 5 …
M12-S4-A3	… 3 ~ 7 ~ 11 …			M12-S0-A6	… 6 …
M12-S6-A0	… 0 ~ 6 …	period = 2		M12-S0-A7	… 7 …
M12-S6-A1	… 1 ~ 7 …			M12-S0-A8	… 8 …
M12-S6-A2	… 2 ~ 8 …			M12-S0-A9	… 9 …
M12-S6-A3	… 3 ~ 9 …			M12-S0-A10	… 10 …
M12-S6-A4	… 4 ~ 10 …			M12-S0-A11	… 11 …
M12-S6-A5	… 5 ~ 11 …

There are additional listings for some primes (table 2D) and composites (table 2E). If m represents the modulus, and positive integer f is a factor of m, then there will be sequences whose period is m ÷ f.

Students of abstract algebra will observe properties of the cyclic groups.

§2-6. As forming modular-linear sequences is the whole point of the game, players will benefit from practice in calculating them:

table 2F — exercises
determine the modulus	problems A	solutions A	each problem will have exactly one solution
extend both ends	problems B	solutions B
fill 1-tile gap	problems C	solutions C	each problem may have multiple solutions, one, or none
fill 2-tile gap	problems D	solutions D
fill 3-tile gap	problems E	solutions E
fill 4-tile gap	problems F	solutions F

The quantity of solutions in the gap-filling case is predictable. Define these symbols:

• m = the modulus;
• g = 1 plus the number of vacancies in the gap;
• f = the greatest common divisor of m and g;
• d = the difference between the first and last values.

• If d is a multiple of f, the problem has at least one solution; otherwise it has none. (Remember that zero is a multiple of any integer.)
• If there are solutions, the quantity of them is equal to f.

For instance, consider 7 ~ x ~ y ~ 6 with modulus 10:

• m = 10
• g = 1 + 2 = 3
• f = 1
• d = 1

In the case where the modulus is a prime number, there will always be a unique solution.

§3. With equipment and sequences explained, here is how to play the game.

§3-1. Preliminaries.

Players need to negotiate:

• what size and shape of board will be employed;
• what the modulus will be, and how many tiles of each number will be used;
• how many tiles each player will maintain in their hand while supplies last;
• which player will go first, second, and so forth — the turn passes from one player to the next in a consistent sequence;
• any custom rules.

After all is agreed on, players turn all the tiles face down on a table and scramble them, to form the stock. Then each takes the agreed-upon quantity of tiles from the stock to form their hand, looking at the tiles but keeping their numbers secret from opponents.

§3-2. General principles.

In a turn, each player transfers at least one tile from their hand to an empty cell on the board, but must never rearrange or remove any tiles that were already there when their turn began.

No cell may contain more than one tile.

At the end of each player's turn, it is necessary that every unbroken straight-line chain of tiles on the board be a legal sequence, that is, modular and linear as detailed in §2-4.

A player scores for the full length of every sequence they create, and for the full length of every sequence that they extend. For example, if a player combines four new tiles with three already on the board, forming a 7-tile sequence, it scores 15.

All the tiles that a player adds in one turn must lie in one unbroken straight line — this is called the primary sequence. This sequence may incorporate tiles that were already on the board from the previous turns of any players.

Often tiles of the primary sequence will combine with other tiles already on the board, incidentally forming or extending other unbroken straight lines of tiles oblique to the primary:

• These must conform to the modular-linear rule, and are called secondary sequences.
• The player scores for each secondary sequence created or extended. Scores for primary and secondary sequences are calculated the same way.
• In some cases, the requirement that secondary sequences be modular-linear means that a player will not be able to extend a primary sequence as far as desired.

If a player in their turn adds only one tile and it lies in two or three sequences, the player may (if a decision need be made) choose any one of the sequences to declare primary with the others being secondary.

A sequence cannot "wrap around" from one edge of the board to the opposite edge.

§3-3. The action.

The first player installs a sequence on the board that must pass through the center cell, A0. It may be of positive, negative, or zero slope; and the player can choose which tile of the sequence will reside on A0.

After that, each player in turn either extends a sequence that already exists, or creates a new sequence. At least one added tile must abut at least one tile that was already on the board.

At the end of each turn, a player draws enough tiles from the stock (if any remain) to restore their hand to its full size. Once the stock becomes empty, play continues but players' hands will shrink.

The game ends when every player has frozen:

• A player must freeze when they have no legal play. This rarely occurs unless their hand has run out of tiles and the stock is empty.
• A player may choose to freeze whenever it is their turn. A player might opt for this if they believe, late in the game, that continued play will benefit opponents more than self.

Whoever ends up with the most points is the winner. Ties are possible, but unlikely.

Page 2 (§4-5-6) — examples