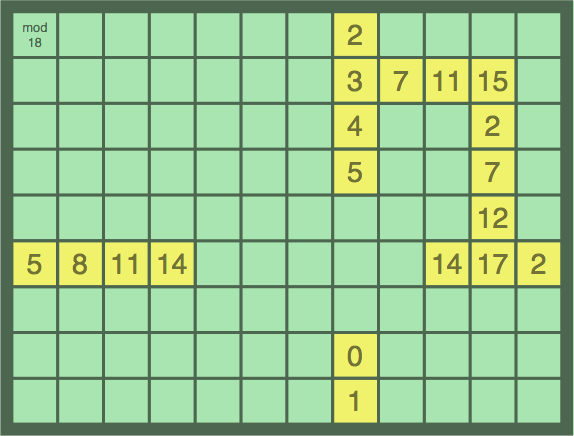
| M18-S4-A3 3 ~ 7 ~ 11 ~ 15 | 4 tiles, 3 points |
| M18-S5-A2 15 ~ 2 ~ 7 ~ 12 ~ 17 | 5 tiles, 6 points |
| M18-S1-A0 0 ~ 1 ~ 2 ~ 3 ~ 4 ~ 5 | 6 tiles, 10 points; wrap |
| M18-S3-A2 14 ~ 17 ~ 2 ~ 5 ~ 8 ~ 11 ~ 14 | 7 tiles, 15 points; wrap |
home page (§1-2-3) — introduction and rules
previous page (§11) — multiplicative variation
next page (§15) — comments
§12. This discussion begins with a digression. Many games are played on a board having a rectangular grid, and some of them allow moves that wrap around the edge of the board. (See toroidal topology.) In fact, MODLINSEQ could easily have been implemented on such a grid — and some players might prefer it that way. In figure 12A there are four ordinary modular-linear sequences as detailed in the table below the image:
| figure 12A | ||||||||
|---|---|---|---|---|---|---|---|---|

| ||||||||
|
In some cases, a wrapped sequence can be connected to form a loop, as in figure 12B. This sequence has 12 tiles and would be worth 55 points, unless players agree to award a loop bonus.
| figure 12B |
|---|
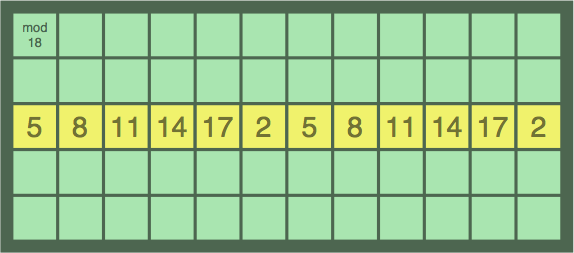
|
In other cases (as with figure 12C), completion of the loop cannot be acheived:
| figure 12C |
|---|
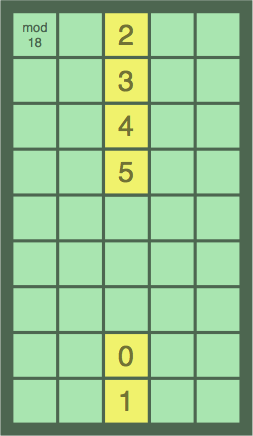
|
A loop becomes possible when the number of cells to be filled is a multiple of the sequence's period.
If diagonal sequences are permitted, they too can wrap. Figure 12D shows 13 ~ 15 ~ 17 ~ 1 ~ 3 ~ 5 ~ 7 ~ 9 ~ 11, worth 28 points:
| figure 12D |
|---|
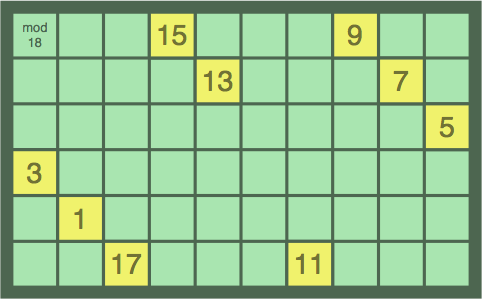
|
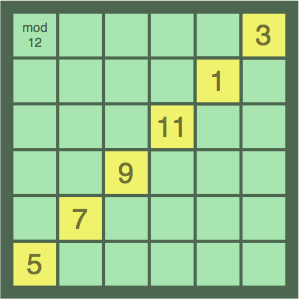
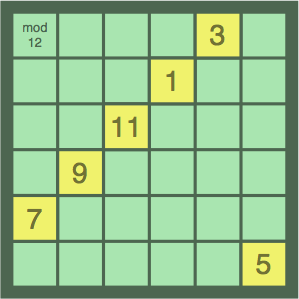
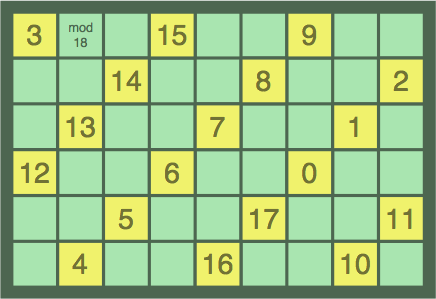
Diagonal loops are possible (figures 12E, 12F, 12G):
| figure 12E 6 tiles, 10 points | figure 12F 6 tiles, 10 points | |
| 
|
| figure 12G 18 tiles, 136 points |
|
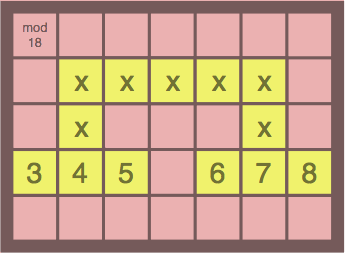
Figure 12H shows an ILLEGAL installation. Although 3 ~ 4 ~ 5 and 6 ~ 7 ~ 8 are valid sequences, they reach opposite edges of the board and therefore must be evaluated as a wrap. Rejection is necessary because 6 ~ 7 ~ 8 ~ 3 ~ 4 ~ 5 is not a good sequence.
| ILLEGAL figure 12H |
|---|
|
In other words, players cannot ignore the fact the the leftmost and rightmost colums are deemed adjacent, as are the top and bottom rows.
§13-1. The digression, which clarified the nature of wrapping around, is now complete; the next step is to extend wrapping to hexagonal boards. Figure 13A includes several sequences that wrap in an unsurprising manner. Despite the scattered appearance, all sequences form one connected network. Cell E7 could hold a 13, but H4 is blocked.
| figure 13A | ||||||||||

| ||||||||||
| ||||||||||
On the order-6 board above, loops of anywhere from 7 tiles (E16 ~ … ~ H16) to 13 tiles (B16 ~ … ~ M16) are possible.
Figure 13B shows how a sequence wraps when it goes into a corner, or follows the edge. Cell B14 is blocked.
| figure 13B | ||||||
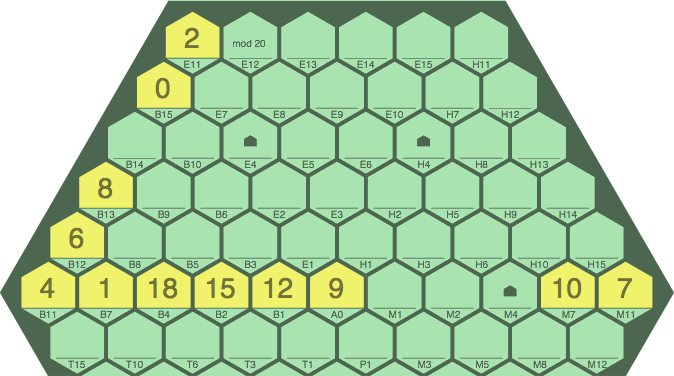
| ||||||
| ||||||
§13-2. Figure 13C introduces the bounce, which is an alternative to the wrap. The image contains five sequences of interest, and nothing wraps around. (In ordinary play, all these sequences would have to be connected by other sequences, but those others are omitted for clarity.)
| figure 13C | ||

| ||
What happens when a sequence reaches the edge of the board? Table 13A lists three cases:
| table 13A referring to figure 13C above | ||
| non‑corner case | situation | A sequence from the interior of the board reaches a cell at the edge of the board that is not a corner cell. |
|---|---|---|
| action | The sequence reflects back into the interior of the board, but not in the direction that it came from. | |
| example | 6 ~ 9 ~ 12 ~ 15 ~ 18 ~ 1 ~ 4, which counts as a 7-tile 15-point sequence. | |
| perimeter case | situation | A sequence installed along the edge of the board reaches a corner. |
| action | The sequence bends, and follows the next edge. | |
| example | 16 ~ 14 ~ 12 ~ 10 ~ 8 ~ 6, which counts as a 6-tile 10-point sequence. | |
| radius case | situation | A sequence coming from interior of the board reaches one of the six cells in a corner. |
| action | The sequence reflects back over itself. | |
| examples | What appears to be 0 ~ 10 ~ 0 ~ 10 is, when written in full, 0T2 ~ 10T4 ~ 0T7 ~ 10T11 ~ 0T7 ~ 10T4 ~ 0T2. Although it employs only 4 physical tiles, it counts as a 7-tile 15-point sequence. | |
| What appears to be 8 ~ 8 ~ 8 is, when written in full, 8P4 ~ 8P7 ~ 8P11 ~ 8P7 ~ 8P4. It counts as a 5-tile 6-point sequence. | ||
| Sequence 6M2 ~ 7M4 ~ 8M7 is valid, but it blocks cell M11. The only value that might work is 9, but then by reflection M7 would have to contain 10, M4 contain 11, and M2 contain 12. | ||
| comment | The only sequences that succeed in the radius case are those with a step of zero; or, when the modulus is even, a step of half the modulus. | |
§14-1. Figure 14A displays an ordinary order-6 board which includes the white cells used for bonuses and maluses. Although the wrap-around scheme of §13-1 could be used here, the white cells would no longer effectively be evenly spaced, which might be regarded as inelegant. For example, there are six plain cells between B6 and H20, which is normal. However, the wrapped sequence H12 ~ H18 ~ B20 has only one plain cell between whites, while A0 ~ M1 ~ … ~ M11 ~ M16 ~ B16 ~ B11 ~ … B1 ~ A0 has twelve.
| figure 14A | ||
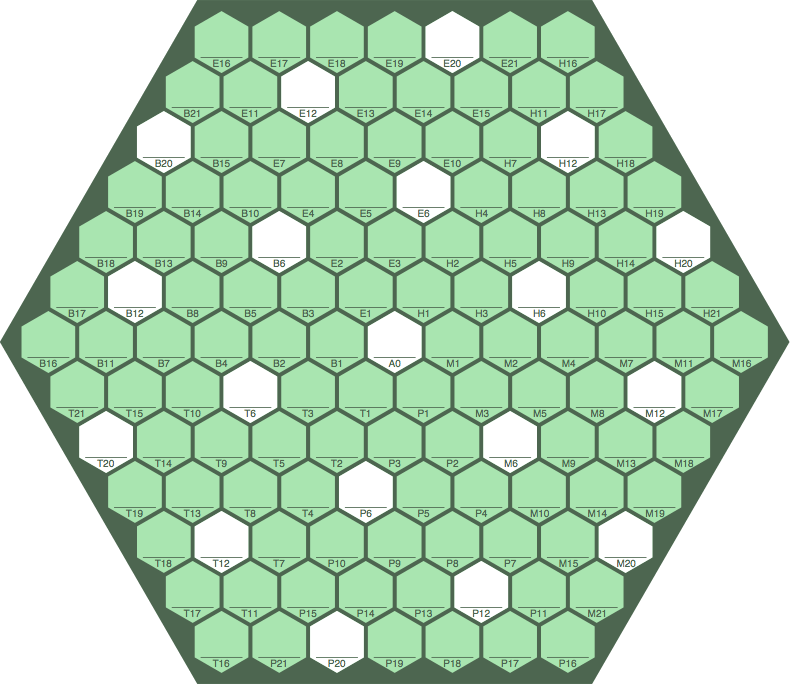
| ||
A better scheme for wrapping around in the bonus/malus environment requires several steps to develop, as follows.
The board above has 127 cells: 19 white and 108 plain. Figure 14B below displays a similar board, termed tess-3 because of its shape and size, with 133 (= 7 × 19) cells: 19 white and 114 plain. Each green cell is adjacent to one white cell; each white adjacent to six green. Ordinary non-wrapping MODLINSEQ could be played on this board, but that is not the purpose in showing it here.
| figure 14B | ||
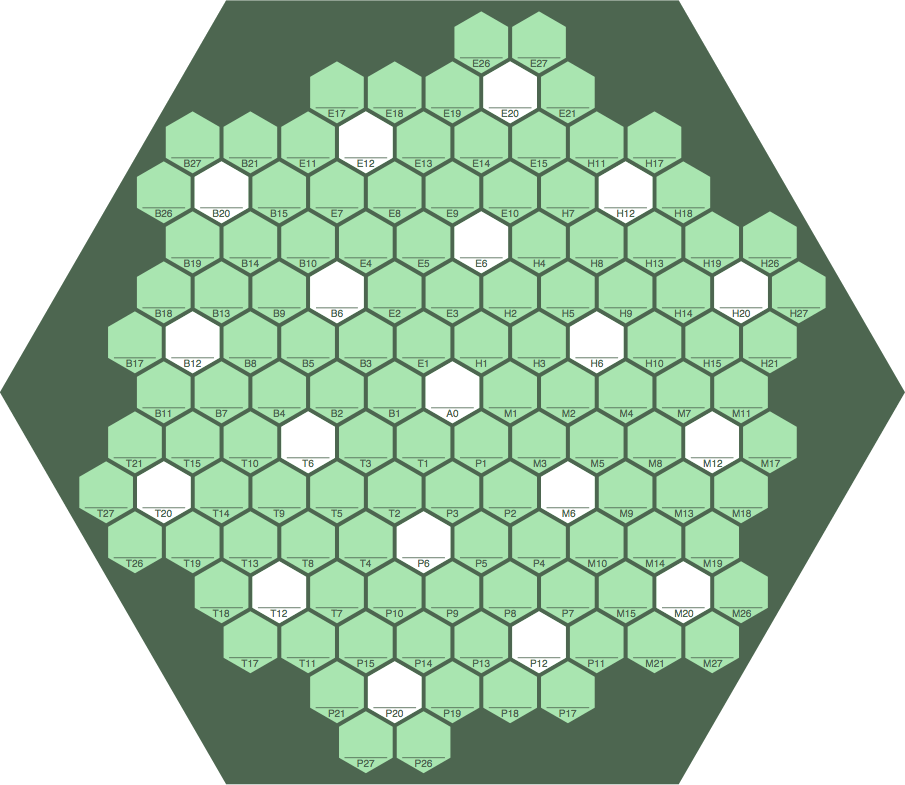
| ||
In figure 14C below, the actual playing area of a tess-2 board is formed by the green cells and the white cells they envelop. A tess-2 board is like the tess-3 board in 14B except in having 49 (= 7 × 7) cells instead of 133. The green tess-2 board in 14C is surrounded by equivalent boards in pink and purple to demonstrate that the tess-2 shape tessellates. The image is rendered at a smaller scale than most others because it contains so many cells; still, it reveals that the periodicity of white cells is undisturbed as it passes from one copy of the board to the next.
| figure 14C | ||
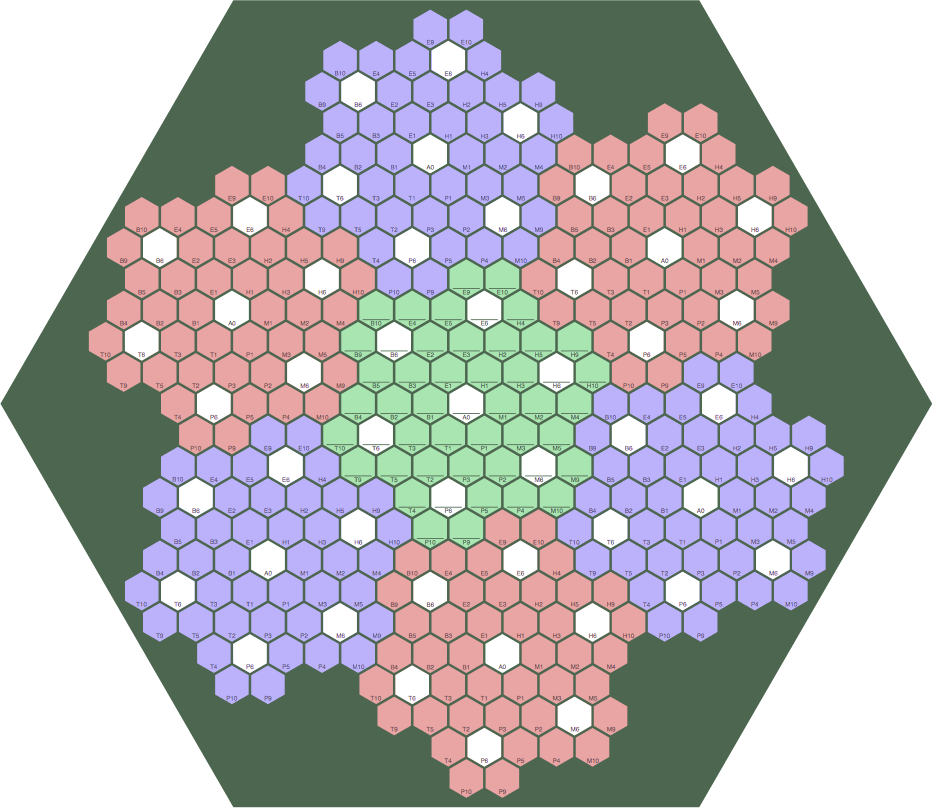
| ||
Returning to normal scale, figure 14D is a slightly modified excerpt of 14C. It continues to show the tess-2 board's playing area in green and white, now surrounded by one wythe of pseudocells, colored in red and bearing an X to emphasize that no tile can be installed on them. The purpose of the pseudocells is to indicate, by their pseudoaddresses, where a wrapped sequence is to continue.
| figure 14D | ||
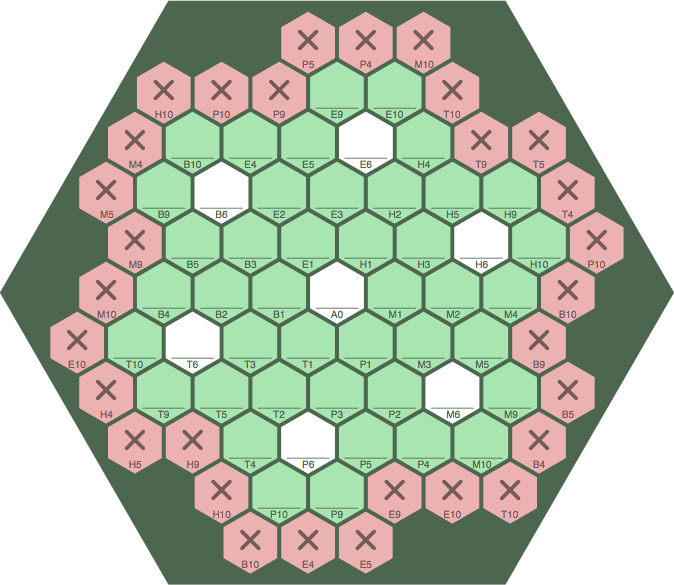
| ||
Although the tess-2 board is too small for advanced play, it is big enough to show how wrapping works. For instance, pseudocell B10 is to the immediate right of cell M4, and — correspondingly — cell B10 is to the immediate right of pseudocell M4. Despite appearing disconnected at first glance, there is only one sequence, having 18 tiles, in figure 14E. If this primary sequence is extended far enough (not likely in uncontrived play) numerous secondary sequences will be formed, some of which may wrap in their own right.
| figure 14E | ||
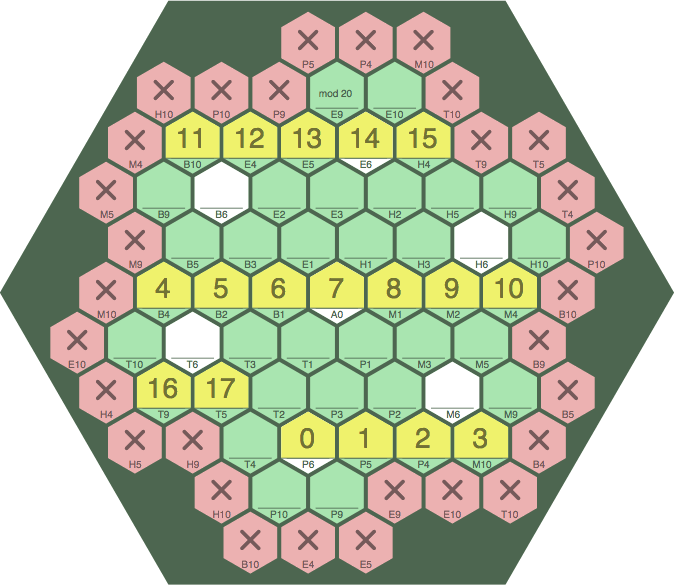
| ||
When a sequence wraps, it never changes slope, but a wrapped sequence can appear equally well in any of the three slopes (compare figures 14E, zero slope; and figure 14F, positive slope).
| figure 14F | ||
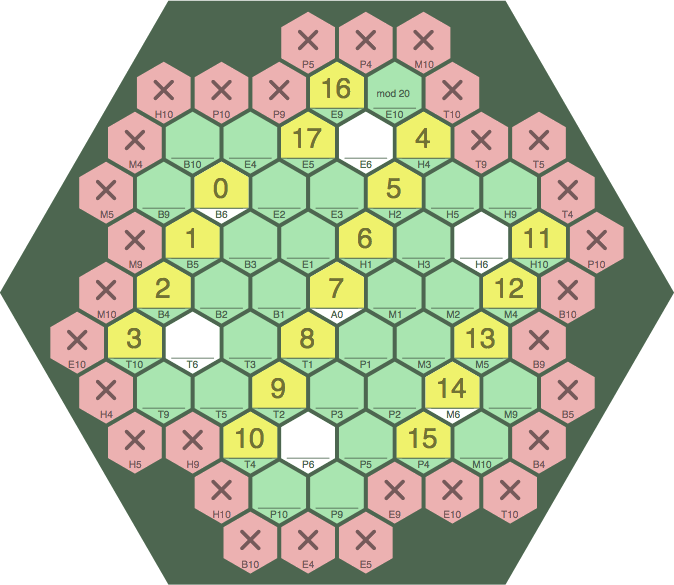
| ||
Figure 14G has one 12-tile sequence, in negative slope.
| figure 14G | ||
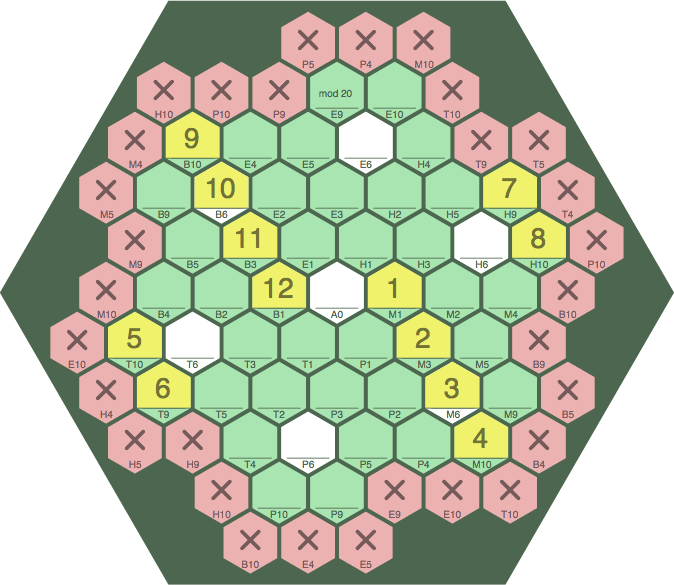
| ||
The tess-n boards are designed so that as many things are "in phase" as possible. An outcome of this is that the modulus-7 installation in figure 14H is legitimate, and can be described as any one of these 49-tile sequences that loops:
| … 0A0 | ~ 1M1 | ~ 2M2 | ~ 3M4 | ~ 4B10 | ~ 5E4 | ~ 6E5 | … |
| … 0A0 | ~ 2T1 | ~ 4T2 | ~ 6T4 | ~ 1H10 | ~ 3M4 | ~ 5M5 | … |
| … 0A0 | ~ 3P1 | ~ 6P2 | ~ 2P4 | ~ 5E10 | ~ 1H4 | ~ 4H5 | … |
Of course, such density will rarely arise in ordinary game play.
| figure 14H | ||

| ||
The tess-3 board in figure 14I, with 133 cells, is a likely choice for play:
| figure 14I | ||
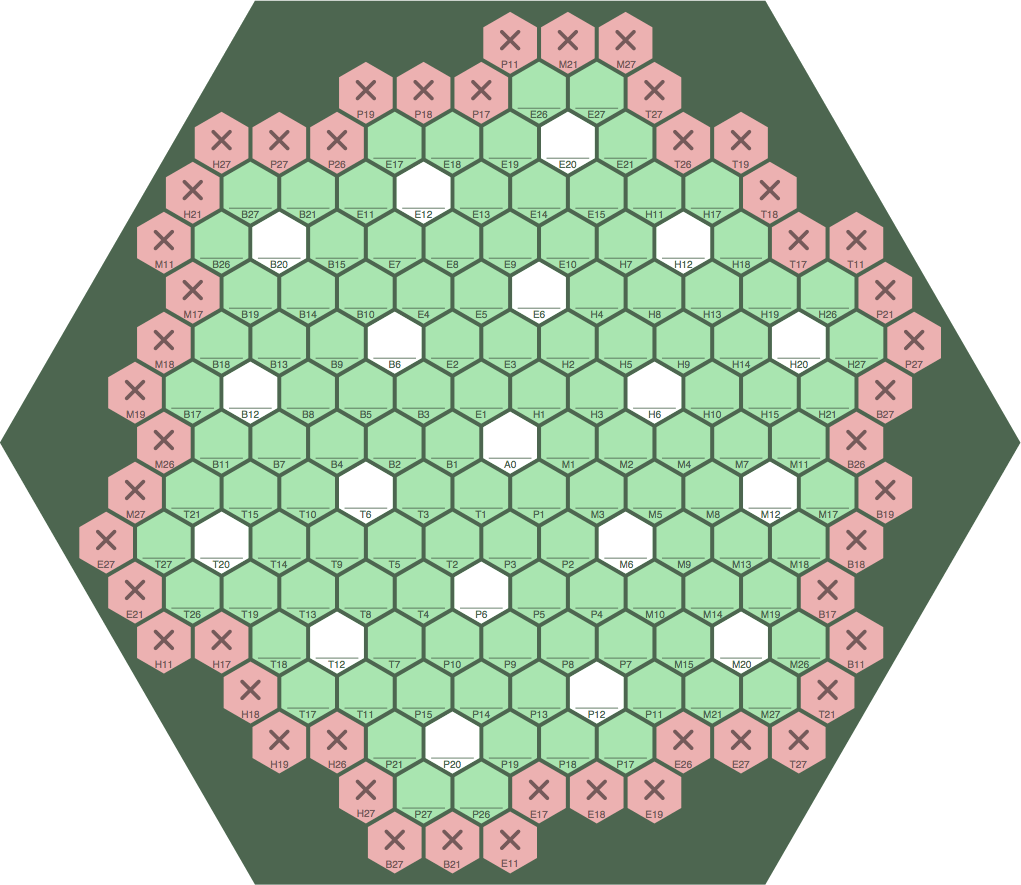
| ||
Because of its size, the tess-4 board is shown on a separate page.
next page (§15) — comments