home page (§1-2-3) — introduction and rules
previous page (§10) — fibonacciësque variation
next page (§12-13-14) — wrap-around variation
§11-1. The modular-linear sequences presented in §2-1 can be described using addition in both directions. Another approach employs multiplication instead, and it works quite satisfactorily for prime moduli.
All tiles with positive numbers less than the modulus remain in use, but tiles bearing the number zero are omitted because that number's annihilativity ruins multiplicative sequences.
The following example from modulus 17 is exactly one period of a sequence:
… 1 ~ 2 ~ 4 ~ 8 ~ 16 ~ 15 ~ 13 ~ 9 …
There are two equally valid ways of calculating it:
The double-ended arrow is useful in notating that 2 and 9 are complementary factors: 2 ↔ 9. Table 11A lists all the complementary factors, along with the periods of the associated sequences, for modulus 17. As with other moduli, the factors and periods do not fall into a conspicuous pattern.
| table 11A | |||||||
|---|---|---|---|---|---|---|---|
| factors | period | factors | period | factors | period | ||
| 1 ↔ 1 | 1 | 4 ↔ 13 | 4 | 10 ↔ 12 | 16 | ||
| 2 ↔ 9 | 8 | 5 ↔ 7 | 16 | 11 ↔ 14 | 16 | ||
| 3 ↔ 6 | 16 | 8 ↔ 15 | 8 | 16 ↔ 16 | 2 | ||
Table 11B (which resembles table 2D and table 2E) contains multiplicative sequences for the prime moduli that are most likely to be of use to game players.
§11-2. Here is an example of how a composite modulus leads to difficulty. Consider the following sequence under modulus 10; exactly one period is shown:
… 8 ~ 6 ~ 2 ~ 4 …
This can be described with a forward factor of either 2 or 7, and a backward factor of either 3 or 8. However, this ambiguity is not the problem. Rather, it is possible for a sequence to originate with one or more terms that are consistent with the forward factor, but inconsistent with any backward factor. Here are some examples with a forward factor of two:
| 9 ~ 8 ~ 6 ~ 2 ~ 4 … |
| 7 ~ 4 ~ 8 ~ 6 ~ 2 ~ 4 … |
| 1 ~ 2 ~ 4 ~ 8 ~ 6 ~ 2 ~ 4 … |
| 3 ~ 6 ~ 2 ~ 4 ~ 8 ~ 6 ~ 2 ~ 4 … |
There can be an ellipsis on only one end, as any backward factor would have to transform an even number into an odd number, which cannot happen with an even modulus. Continuing with a forward factor of 2, an attempt to start a sequence with 5 fares no better:
5 ~ 0 ~ 0 ~ 0 …
Modulus 10 can be made to work if factors are limited to 1 ↔ 1, 3 ↔ 7, and 9 ↔ 9. The greatest common divisor function reveals why these succeed; gcd (1, 10), gcd (3, 10), gcd (7, 10), and gcd (9, 10) all equal 1. Although modulus 10 is not likely to result in a satisfying game, table 11C nonetheless shows what sequences would be extensible on both ends.
| table 11C — modulus 10 | ||||
|---|---|---|---|---|
| 1 ↔ 1 | … 1 … | … 2 … | … 3 … | |
| … 4 … | … 5 … | … 6 … | ||
| … 7 … | … 8 … | … 9 … | ||
| 3 ↔ 7 | … 1 ~ 3 ~ 9 ~ 7 … | … 2 ~ 6 ~ 8 ~ 4 … | ||
| 3 ↔ 7 | … 5 … | |||
| 9 ↔ 9 | … 1 ~ 9 … | … 2 ~ 8 … | … 3 ~ 7 … | … 4 ~ 6 … |
| 9 ↔ 9 | … 5 … | |||
§11-3. A one-to-one correspondence can be established between the additive sequences of modulus p − 1, and the multiplicative sequences of modulus p, where p is prime. Here is a detailed example, using additive modulus 10 and multiplicative modulus 11. Table 11D below is taken from tables 2E and 11B. Within each side of the table, the rows have been arranged in what will turn out to be a convenient order.
| table 11D | ||||
|---|---|---|---|---|
| additive modulus 10 | multiplicative modulus 11 | |||
| M10-S0-A0 | … 0 … | 1 ↔ 1 | … 1 … | |
| M10-S0-A1 | … 1 … | 1 ↔ 1 | … 2 … | |
| M10-S0-A2 | … 2 … | 1 ↔ 1 | … 4 … | |
| M10-S0-A3 | … 3 … | 1 ↔ 1 | … 8 … | |
| M10-S0-A4 | … 4 … | 1 ↔ 1 | … 5 … | |
| M10-S0-A5 | … 5 … | 1 ↔ 1 | … 10 … | |
| M10-S0-A6 | … 6 … | 1 ↔ 1 | … 9 … | |
| M10-S0-A7 | … 7 … | 1 ↔ 1 | … 7 … | |
| M10-S0-A8 | … 8 … | 1 ↔ 1 | … 3 … | |
| M10-S0-A9 | … 9 … | 1 ↔ 1 | … 6 … | |
| M10-S5-A0 | … 0 ~ 5 … | 10 ↔ 10 | … 1 ~ 10 … | |
| M10-S5-A1 | … 1 ~ 6 … | 10 ↔ 10 | … 2 ~ 9 … | |
| M10-S5-A2 | … 2 ~ 7 … | 10 ↔ 10 | … 4 ~ 7 … | |
| M10-S5-A3 | … 3 ~ 8 … | 10 ↔ 10 | … 3 ~ 8 … | |
| M10-S5-A4 | … 4 ~ 9 … | 10 ↔ 10 | … 5 ~ 6 … | |
| M10-S2-A0 | … 0 ~ 2 ~ 4 ~ 6 ~ 8 … | 3 ↔ 4 | … 1 ~ 3 ~ 9 ~ 5 ~ 4 … | |
| M10-S2-A1 | … 1 ~ 3 ~ 5 ~ 7 ~ 9 … | 3 ↔ 4 | … 2 ~ 6 ~ 7 ~ 10 ~ 8 … | |
| M10-S4-A0 | … 0 ~ 4 ~ 8 ~ 2 ~ 6 … | 5 ↔ 9 | … 1 ~ 5 ~ 3 ~ 4 ~ 9 … | |
| M10-S4-A1 | … 1 ~ 5 ~ 9 ~ 3 ~ 7 … | 5 ↔ 9 | … 2 ~ 10 ~ 6 ~ 8 ~ 7 … | |
| M10-S1-A0 | … 0 ~ 1 ~ 2 ~ 3 ~ 4 ~ 5 ~ 6 ~ 7 ~ 8 ~ 9 … | 2 ↔ 6 | … 1 ~ 2 ~ 4 ~ 8 ~ 5 ~ 10 ~ 9 ~ 7 ~ 3 ~ 6 … | |
| M10-S3-A0 | … 0 ~ 3 ~ 6 ~ 9 ~ 2 ~ 5 ~ 8 ~ 1 ~ 4 ~ 7 … | 7 ↔ 8 | … 1 ~ 7 ~ 5 ~ 2 ~ 3 ~ 10 ~ 4 ~ 6 ~ 9 ~ 8 … | |
Table 11E defines a particular one-to-one correspondence between the sets { 0 … 9 } and { 1 … 10 }. (Certain other correspondences would also have worked.)
| table 11E | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| add { 0 … 9 } | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| mul { 1 … 10 } | 1 | 2 | 4 | 8 | 5 | 10 | 9 | 7 | 3 | 6 |
Table 11F applies 11E to 11D. Within each sequence, the corresponding additive and multiplicative terms are written before and after the slash, producing what might be described as a dual sequence. Most of the rows match exactly; the four exceptions are highlighted in gold. In each of those cases the two dual sequences are the same, but one is written in the reverse notation from the other.
| table 11F | ||
|---|---|---|
| additive modulus 10 | multiplicative modulus 11 | |
| … 0/1 … | … 0/1 … | |
| … 1/2 … | … 1/2 … | |
| … 2/4 … | … 2/4 … | |
| … 3/8 … | … 3/8 … | |
| … 4/5 … | … 4/5 … | |
| … 5/10 … | … 5/10 … | |
| … 6/9 … | … 6/9 … | |
| … 7/7 … | … 7/7 … | |
| … 8/3 … | … 8/3 … | |
| … 9/6 … | … 9/6 … | |
| … 0/1 ~ 5/10 … | … 0/1 ~ 5/10 … | |
| … 1/2 ~ 6/9 … | … 1/2 ~ 6/9 … | |
| … 2/4 ~ 7/7 … | … 2/4 ~ 7/7 … | |
| … 3/8 ~ 8/3 … | … 8/3 ~ 3/8 … | |
| … 4/5 ~ 9/6 … | … 4/5 ~ 9/6 … | |
| … 0/1 ~ 2/4 ~ 4/5 ~ 6/9 ~ 8/3 … | … 0/1 ~ 8/3 ~ 6/9 ~ 4/5 ~ 2/4 … | |
| … 1/2 ~ 3/8 ~ 5/10 ~ 7/7 ~ 9/6 … | … 1/2 ~ 9/6 ~ 7/7 ~ 5/10 ~ 3/8 … | |
| … 0/1 ~ 4/5 ~ 8/3 ~ 2/4 ~ 6/9 … | … 0/1 ~ 4/5 ~ 8/3 ~ 2/4 ~ 6/9 … | |
| … 1/2 ~ 5/10 ~ 9/6 ~ 3/8 ~ 7/7 … | … 1/2 ~ 5/10 ~ 9/6 ~ 3/8 ~ 7/7 … | |
| … 0/1 ~ 1/2 ~ 2/4 ~ 3/8 ~ 4/5 ~ 5/10 ~ 6/9 ~ 7/7 ~ 8/3 ~ 9/6 … | … 0/1 ~ 1/2 ~ 2/4 ~ 3/8 ~ 4/5 ~ 5/10 ~ 6/9 ~ 7/7 ~ 8/3 ~ 9/6 … | |
| … 0/1 ~ 3/8 ~ 6/9 ~ 9/6 ~ 2/4 ~ 5/10 ~ 8/3 ~ 1/2 ~ 4/5 ~ 7/7 … | … 0/1 ~ 7/7 ~ 4/5 ~ 1/2 ~ 8/3 ~ 5/10 ~ 2/4 ~ 9/6 ~ 6/9 ~ 3/8 … | |
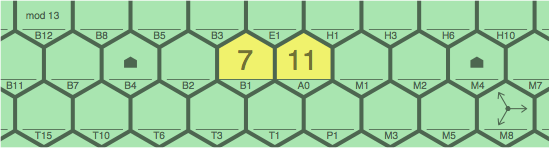
§11-4. This multiplicative variation can be combined with the fibonacciësque variation (§10). An open question is whether strategy and tactics would be enhanced sufficiently to justify the increased complication of calculation. The following modulus-13 example shows what intricacies an obvious adaptation might entail. First installed are 7B1 and 11A0:
| figure 11A |

|
For convenient reference, here is a list of multiples of 13:
| 13, | 26, | 39, | 52, | 65, | 78, | 91, | 104, | 117, | 130, | 143, | 156 |
To calculate M1, figure 7 × 11 yielding 77. The largest multiple of 13 not greater than 77 is 65, so subtract 65 from 77 and install 12M1.
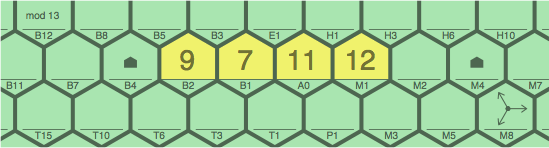
To calculate B2, one would figure 11 ÷ 7, except 11 is not a multiple of 7. Iterating:
| figure 11B |
|
To calculate M2, figure 11 × 12 yielding 132. The largest multiple of 13 not greater than 132 is 130, so subtract 130 from 132 and install 2M2.
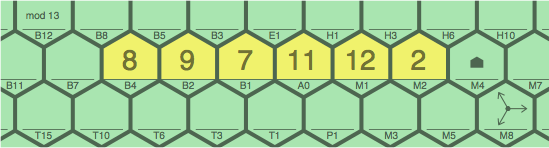
To calculate B4, one would figure 7 ÷ 9, except 7 is not a multiple of 9. Iterating:
| figure 11C |
|
To calculate M4, figure 12 × 2 yielding 24. The largest multiple of 13 not greater than 24 is 13 itself, so subtract 13 from 24 and install 11M4.
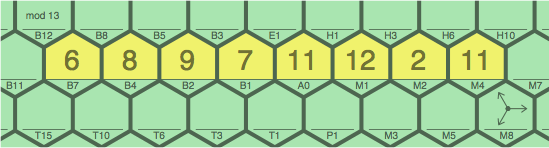
To calculate B7, one would figure 9 ÷ 8, except 9 is not a multiple of 8. Adding 13 each time:
| figure 11D |
|
next page (§12-13-14) — wrap-around variation