28. Introduction. In the 60° and 90° systems, it is easy to find the right length of track to fill a gap. Because the greatest common factor of 60 and 90 is 30, one might ask whether a 30° scheme would itself be simple to use. This page addresses the question.

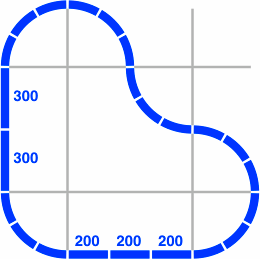
Although overall track width will still be 40mm, circular segments will now be of radius 300mm rather than 200mm. This change is necessary because for a common configuration of switch, a curved segment of radius 200mm will not clear the straight segment. Figure 28-1 illustrates the problem and a solution.

Figure 28-1a 200mm radius; unacceptable	Figure 28-1b 300mm radius; acceptable
scale 4x

The minimum radius to make this switch work is 278.56mm [=140 + 80 × √3], and 300 is a convenient round number. With the 300mm radius, the minimum length of the straight segment is 154.92mm [= √(320² − 280²)], or the straight segment will not clear the curved segment.

In the 30° system, there are twelve segments to a circle. Figure 28-2 contrasts the 200 and 300mm radii.

Figure 28-2a 200mm radius	Figure 28-2b 300mm radius

Corresponding to figure 16-2 is 28-3, which shows that a 30° system will need a straight segment 600mm long, or some equivalent combination of shorter segments.

Figure 28-3

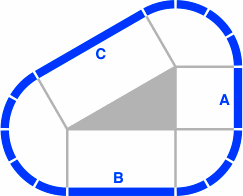
Figure 28-4 contains in gray a 30°-60°-90° triangle, similar in role to figures 20-5 and 20-6 of the 36° system.

Figure 28-4

Elementary trigonometry applied to figure 28-4 says that the length of side C must be twice the length of side A, while the ratio of B to A is √3, approximately 1.73205. Each column of table 28-A gives a few examples of what lengths the three sides can assume. Each number, representing millimeters, is rounded to the nearest integer.

Table 28-A Sides of some triangles
A	50	65	75	87	100	130	150	173	200	260	300	346
B	87	112	130	150	173	225	260	300	346	450	520	600
C	100	130	150	173	200	260	300	346	400	520	600	693

Why can there be so many track lengths in the 30° system? To answer this, we can start with 600mm, which according to figure 28-3 needs to be an attainable length:

• If A = 600, then B = 1039 and C = 1200
• If B = 600, then C = 693 and A = 346
• If C = 600, then A = 300 and B = 520

• placing 1039 or 520 in position A or C
• placing 1200 or 693 in position A or B
• placing 300 or 346 in position B or C

Those lengths will in turn propagate a third round of lengths, et cetera.

The relation of C and A means that given any length, it will need to either doubled or halved to finish the triangle. Similarly, the relation of B and A means that any length requires multiplying or dividing by √3. As a result, a comprehensive table of segment lengths is two-dimensional.

Table 28-B gives the big picture of how the numbers of table 28-A are calculated. Within each box, above the line, are an integer approximation (in bold), a two-place approximation, and an exact expression. Below the line are found two-way and three-way decompositions. The arbitrary starting point is 600 (in the shaded box), from figure 28-2.

Table 28-B Some track lengths
	2−3	2−2	2−1	20	2+1
3−1.0	25 25.00 600 × 2−3 × 3−1.0 13 + 13 8 + 8 + 8	50 50.00 600 × 2−2 × 3−1.0 25 + 25 17 + 17 + 17	100 100.00 600 × 2−1 × 3−1.0 50 + 50 33 + 33 + 33	200 200.00 600 × 20 × 3−1.0 100 + 100 67 + 67 + 67	400 400.00 600 × 2+1 × 3−1.0 200 + 200 133 + 133 + 133
3−0.5	43 43.30 600 × 2−3 × 3−0.5 22 + 22 14 + 14 + 14	87 86.60 600 × 2−2 × 3−0.5 43 + 43 29 + 29 + 29	173 173.21 600 × 2−1 × 3−0.5 87 + 87 58 + 58 + 58	346 346.41 600 × 20 × 3−0.5 173 + 173 115 + 115 + 115	693 692.82 600 × 2+1 × 3−0.5 346 + 346 231 + 231 + 231
30	75 75.00 600 × 2−3 × 30 38 + 38 25 + 25 + 25	150 150.00 600 × 2−2 × 30 75 + 75 50 + 50 + 50	300 300.00 600 × 2−1 × 30 150 + 150 100 + 100 + 100	600 600.00 600 × 20 × 30 300 + 300 200 + 200 + 200	1200 1200.00 600 × 2+1 × 30 600 + 600 400 + 400 + 400
3+0.5	130 129.90 600 × 2−3 × 3+0.5 65 + 65 43 + 43 + 43	260 259.81 600 × 2−2 × 3+0.5 130 + 130 87 + 87 + 87	520 519.62 600 × 2−1 × 3+0.5 260 + 260 173 + 173 + 173	1039 1039.23 600 × 20 × 3+0.5 520 + 520 346 + 346 + 346	2078 2078.46 600 × 2+1 × 3+0.5 1039 + 1039 693 + 693 + 693

The table is two-dimensional in structure, in contrast to the primary series of the 45° system and the alpha series of the 36° system, which are one-dimensional.

Feasible lengths run from about 40mm to 800mm, but others are included to make the pattern clearer; the table can easily be extended to higher or lower powers of 2 or √3. Such extension will however reveal the inconvenient fact that, because √3 ÷ 2 is irrational, the quantity of lengths that can be produced in the feasible range is unbounded. Even more, the set of numbers obtainable by extending table 28-B are dense among the reals. What this means is that any nonnegative real number can be approximated arbitrarily closely by a number of the form 600 × 2^m × 3^n÷2, with m and n integer.

Of some mitigation is that any segment may be partitioned into two or three equal lengths: this aids in reducing the number of different lengths needed for practical use. Unfortunately, no small selection of the possible values is conspicuous as a working subset.

29. Figure-eights. Of these, there are five that are fundamental.

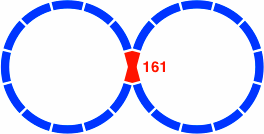
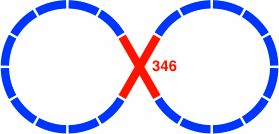
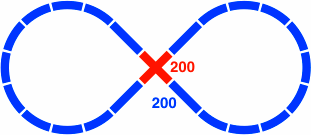
Figure 29-1 11 curved segments per lobe 161 = 600 × tan15° ≠ 600 × 2m × 3n÷2	Figure 29-2 10 curved segments per lobe 346 = 600 × tan30° = 600 × 20 × 3−0.5
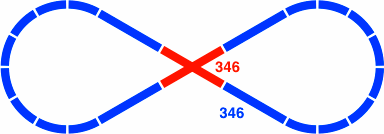
Figure 29-3 9 curved segments per lobe 600 = 600 × tan45° = 600 × 20 × 30	Figure 29-4 8 curved segments per lobe 1039 = 600 × tan60° = 600 × 20 × 3+0.5
Figure 29-5 7 curved segments per lobe 2239 = 600 × tan75° = 600 × 2+1 × 30 + 600 × 20 × 3+0.5

The following layouts substitute shorter segments for longer ones:

Figure 29-6 variant of 29-3	Figure 29-7 variant of 29-4

The crossing piece in 29-7 is the same as that of 29-2. Although not illustrated, similar decompositions can be devised for the layout of figure 29-5 because 2239 = 1200 + 1039, both of which addends are found in table 28-B. An example is the breakdown 2239 = 1039 + 161 + 1039, which uses the same crossing as 29-1.

The length of the segments in the crossing of figure 29-1 is not an entry in table 28-B; rather, it is the difference between two entries: 161 = 1200 − 1039. Whether this distance might be the sum of finitely many entries is not yet known. In any case, pieces much shorter would not clear each other, because the minimum length is 149.28mm [= 40 ÷ tan15°].